Aufgabe:
16. Flächeninhalt Die Abbildung rechts zeigt den Graphen von \( f(x)=4 x e^{-0,5 x} \)
Die Normale \( n \) im Wendepunkt \( W\left(4 \mid \frac{16}{e^{2}}\right) \) hat die
Gleichung \( \mathrm{n}(\mathrm{x})=\frac{\mathrm{e}^{2}}{4} \mathrm{x}-\mathrm{e}^{2}+\frac{16}{\mathrm{e}^{2}} \)
a) Zeigen Sie, dass \( \mathrm{F}(\mathrm{x})=(-8 \mathrm{x}-16) \mathrm{e}^{-0,5 \mathrm{x}} \) eine
Stammfunktion von \( \mathrm{f} \) ist.
b) Berechnen Sie den Inhalt der markierten Fläche.
Problem/Ansatz:
Aufgabe A habe ich bereits gelöst, aber bei Aufgabe B komme ich nicht weiter:
Ich dachte mir ich berechne erst die Schnittstellen von n(x) und f(x) aber ehrlich gesagt komme ich schon da nicht weiter und bin mir auch nicht sicher ob das der richtige Ansatz ist. Denn ich würde dann ja nicht nur die Fläche berechnen die ich berechnen soll, sondern alles (siehe Bild). Ist es stattdessen besser die Nullstelle von n(x) zu berechnen? Aber wie rechne ich dann damit weiter? Berechnen soll ich nur die schwarze Fläche.
Ich würde mich sehr über Hilfe freuen!
LG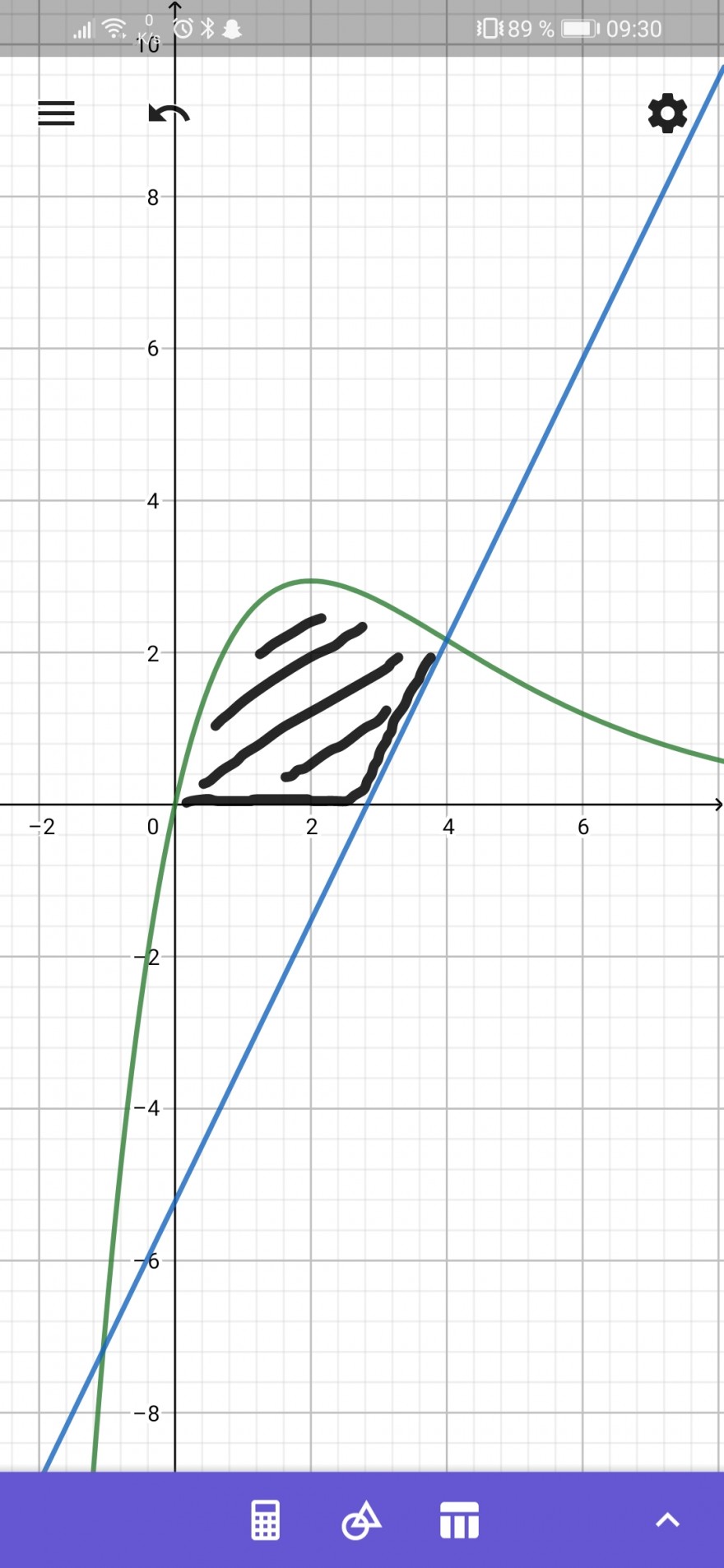
Text erkannt:
8)