Wenn Schüler*innen von sich sagen, dass sie eine mathematische Aussage verstanden haben, meinen sie im Allgemeinen, dass sie Fälle der Anwendbarkeit eines mathematischen Satzes identifizieren und von denen unterscheiden können, in denen keine Anwendbarkeit vorliegt. Weiterhin meinen sie auch, dass sie die Algorithmen der Anwendungen beherrschen. In diesem Sinne verwenden auch viele Internet-Portale (z.B. ‚Lernen mit Lehrer Schmidt‘, ‚Schlau mit Wow‘) den Begriff des Verstehens.
Ein guter Mathematikunterricht will aber mehr. Es will Schüler*innen Einsicht in das ‚Warum‘ der Gültigkeit einer mathematischen Aussage vermitteln. Diese Einsicht kann durch geeignete Lehrerfragen angeregt und dann selbständig gewonnen werden. Auch kann sie über das Verstehen eines Beweises der in Frage stehenden Aussage gewonnen werden – muss aber nicht. So kann beispielsweise eine Einsicht in das ‚Warum‘ der Gültigkeit eines Strahlensatzes über Beobachtungen in der Lebenswelt gewonnen werden. Es genügt, Schattenlängen als proportional zu den Höhen der schattenwerfenden Objekte zu erleben. Ein mathematischer Beweis eines Strahlensatzes gelingt zum Zeitpunkt seiner Einführung mit den zu diesem Zeitpunkt zur Verfügung stehenden mathematischen Mitteln noch nicht.
In Schulbüchern findet man die Plausibilisierung eines Strahlensatzes über äquidistante Parallelenscharen, auf denen der Startpunkt der Strahlen ebenso liegt, wie die Schnittpunkte mit den genannten Parallelen. Dieser Erlärungsversuch lässt die Fälle unberücksichtigt, in denen ein gemeinsames Maß der abzuzählenden Anzahlen der Parallelen der Schar nicht existiert. Sowohl in einer Messreihe dokumentierte Beobachtungen beim Schattenwurf als auch eine Darstellung innerhalb einer Schar äquidistanter Parallelen sind geeignet, in den Köpfen der Schüler*innen eine Reaktion auszulösen, die weitgehend selbständig erfolgt und die man als ‚Verstehen‘ bezeichnen könnte.
Ein guter im Mathematikunterricht schafft Gelegenheiten zum selbständigen Entdecken und verhilft so zu der Einsicht in das ‚Warum‘ einer mathematischen Aussage. Solche Gelegenheiten erfordern sorgfältige Planung auf der Seite der Unterrichtenden. Das selbständige Entdecken des zweiten Strahlensatzes kann zum Beispiel auf folgendem Wege angeregt werden:
Schneide in einen Karton in DINA-4 Format ein rechteckiges Loch der Höhe 5 mm und der Breite 2 mm. Montiere diesen Karton sowie einen zweiten (hellen) Karton an den Enden eines ca. 1 m langen zu den Kartons senkrechten Stabes. Richte bei Sonnenschein den Stab auf die Sonne:
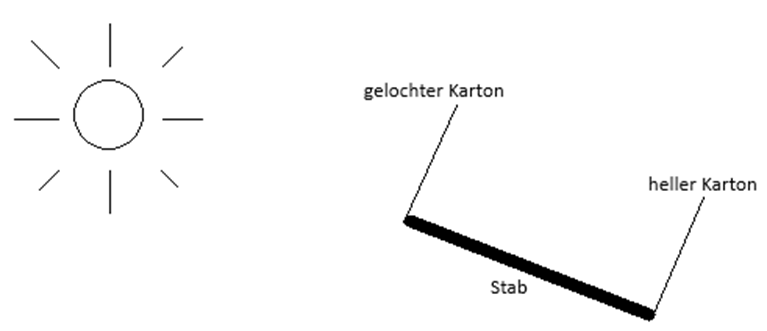
Halte einen weiteren hellen Karton zwischen beide Kartons parallel zu diesen und verschiebe ihn entlang des Stabes. Beobachte den Schattenwurf auf diesem Karton. Notiere deine Beobachtungen.
Einige Schüler*innen werden notieren:
- Beim Abstand a< 10 cm zwischen gelochtem und drittem Karton erscheint ein helles Fast-Rechteck auf dem dritten Karton.
- Ohne den dritten Karton erscheint ein heller Kreis auf dem hellen Karton.
Die Begründungen für diese Beobachtungen werden im Unterrichtsgespräch erarbeitet. Insbesondere muss der Übergang vom hellen Rechteck zum hellen Kreis begründet werden. Ziel des Unterrichtsgespräches ist die Entdeckung: Der Kreis hat die Form der Lichtquelle (Sonne) und kann als das Bild er Sonne verstanden werden. Daraufhin erhalten die Schüler*innen den Auftrag, das Verhältnis aus Entfernung zur Sonne zu ihrem Durchmesser im Netz zu recherchieren und mit dem Verhältnis aus Kartonabstand zu Durchmesser des hellen Kreises zu vergleichen.
Im Zuge dieses Vorgehens wird sicher eine erste Formulierung des zweiten Strahlensatzes von Schüler*innen genannt.
