Verschieben einer Parabel g in y-Richtung, damit sie Parabel f berührt

Question

F(x)=-x^2-3x g(x)= 0.5x(x+3) verschieben sie die Parabel G von g in y richtung so , dass die verschobenen parabel k von f berührt. Bestimmen sie die Koordinaten des berührpunktes.

Answer 1

Hallo lola_lala,

 

schöne, aber schwierige Aufgabe :-)

Wir haben

f(x) = -x² - 3x und

g(x) = 0,5x * (x + 3) = 0,5x² + 1,5x

 

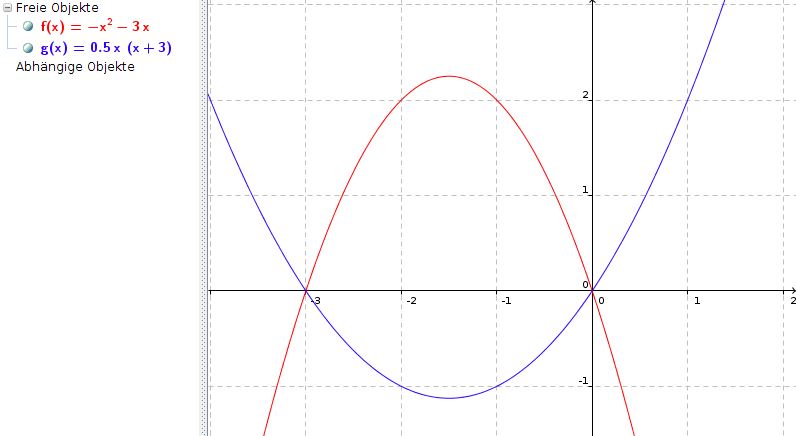
Die Parabel von g(x) soll so in y-Richtung verschoben werden, dass sie die Parabel von f(x) berührt.

Am Berührpunkt muss g(x) den gleichen Anstieg haben wie f(x), also

f'(x) = -2x - 3 = g'(x) = x + 1,5

-3x = 4,5

x = -1,5

 

Die beiden Graphen berühren sich also nach der entsprechenden Verschiebung an der Stelle x = -1,5

Wie lauten die Funktionswerte von f(x) und g(x) an der Stelle x = -1,5?

f(-1,5) = -2,25 + 4,5 = 2,25

g(-1,5) = 1,125 - 2,25 = -1,125

Also muss der Graph von g(x) um 2,25 - (-1,125) = 3,375 Stellen nach oben verschoben werden, um den Graphen von (fx) an der Stelle (-1,5|2,25) zu berühren.

 

Dann lautet die Funktionsgleichung des verschobenen Graphen

g₁(x) = 0,5 * (x + 3) + 3,375

Die 3,375 könnte man natürlich noch in die Klammer ziehen :-D

 

 

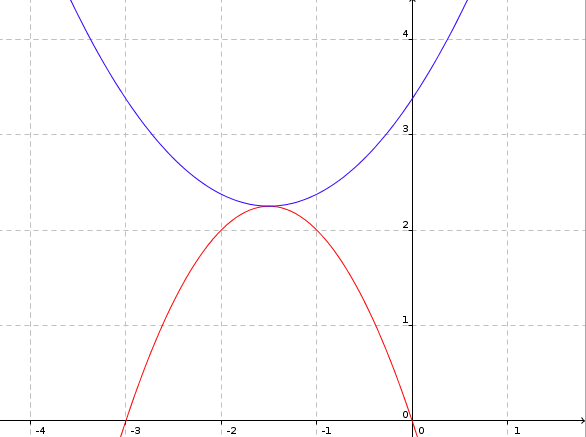
Besten Gruß