3*log(x^5)=log(x^15)
5*log(x^2)=log(x^10)
log(x^15)-log(x^10)=log(x^5)
log(x^5)=1,50515
5*log(x)=1,50515
log(x)=0,30103
x≈1,35125 , wenn log der natürliche Logarithmus ist.
x≈2 ,wenn log(x) mit der Basis 10 gemeint ist.
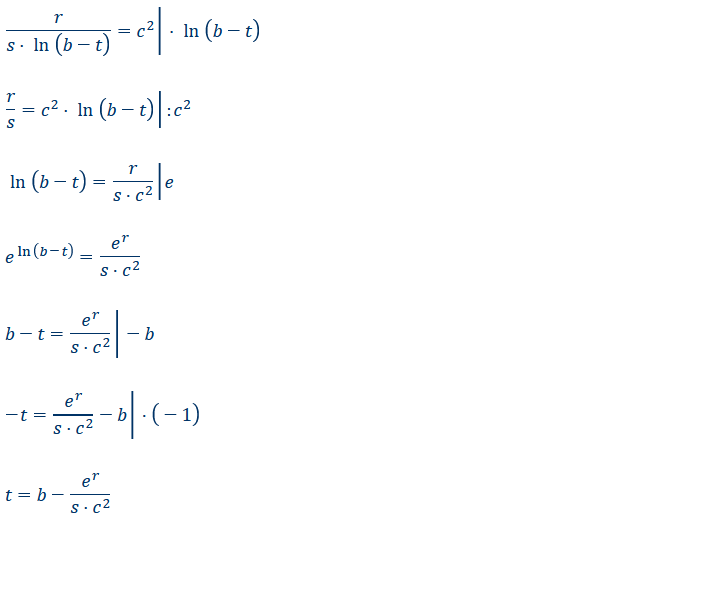
Text erkannt:
\( \frac{r}{s \cdot \ln (b-t)}=c^{2} \mid \cdot \ln (b-t) \)
\( \frac{r}{s}=c^{2} \cdot \ln (b-t) \mid: c^{2} \)
\( \ln (b-t)=\frac{r}{s \cdot c^{2}} \mid e \)
\( e^{\ln (b-t)=\frac{e^{r}}{s \cdot c^{2}}} \)
\( b-t=\frac{e^{r}}{s \cdot c^{2}} \mid-b \)
\( t=b-\frac{e^{r}}{s \cdot c^{2}} \)