Berechne die fehlenden Größen mit allen Rechenschritten Bei einem pyramidenförmigen Zelt mit quadratischer …

Question

Text erkannt:

Berechne die fehlenden Größen mit allen Rechenschritten Bei einem pyramidenförmigen Zelt mit quadratischer Grundfläche ist eine Seitenstange und der Reißverschluss vorne kaputt gegangen.
a) Berechne die Länge der Seitenstange.
b) Berechne die Länge des Reißverschlusses (vorne)
c) Außerdem soll das Zelt imprägniert werden. (Seitenwände und Boden) Eine Dose Imprägnierspray reicht für \( 4 \mathrm{~m}^{2} \). Wie viele Dosen werden benötigt

Aufgabe:

die Aufgabe ist im Anhang,ich bitte um ihre Hilfe, schnellstmöglich

Vielen Dank ;-)

Comments

Bitte die beschrifteten Längen im Bild als Text angeben.

Zudem: Wie verlaufen die Seitenstangen, damit es dort nicht reinregnet? Von der Zeltspitze zur Ecke oder dem Boden entlang?

---

Was soll ich denn bitte beschriften?,und vor allem sind die Größen auch klar auf'm Bild erkennbar,nur die eine Einheit ganz oben ist nicht beschriftet

Mfg

Answer 1

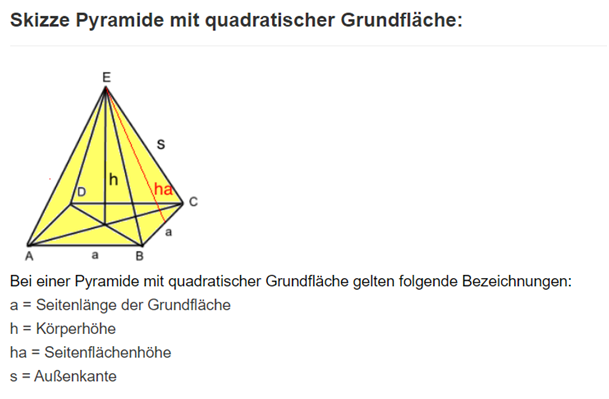
Gegeben: quadratische Pyramide
a = 3m
h = 2m
Gesucht: a) Berechne die Länge der Seitenstange(s)

b) Länge Reißverschluss(ha)

Über folgende Beziehung (Satz des Pythagoras) kann s berechnet werden:

Länge Reißverschluss:
ha² =  h² + (a/2)²
ha =√(h² + (a/2)²    )
ha =√(2² + (3/2)²    )
ha = 2,5 m

Außenkante:
s² =  ha² + (a/2)²    oder s² =  h² + (d/2)²  wobei d = a * √2 (d = Diagonale Grundfläche)

Seitenstange:
s = √(ha² + (a/2)²    ) = √(2,5²+(3/2)²)
s ≈ 2,92 m
c)   

Oberfläche: O = Gf +  M
Mantel: M = a * ha * 2
Grundfläche: Gf = a²
M = 3*2,5*2

M= 15 m²

Gf = 3² = 9 m²

O = 24 m²

4m² je Dose

Dosenanzahl = O :4 = 24 m² :4 = 6 Dosen

Comments

Dankeschön, vielmals :-)