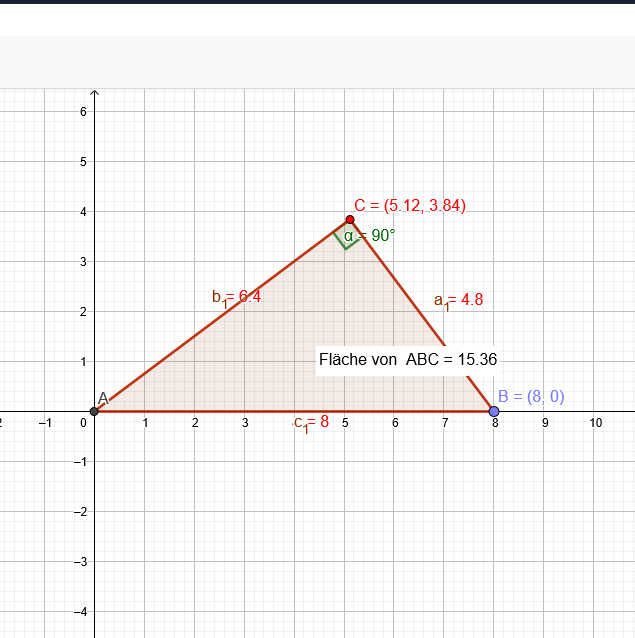
Berechne den Umfang und den Flächeninhalt der Figur(Dreieck).

Question

Aufgabe:

Berechne den Umfang und den Flächeninhalt der Figur(Dreieck). Runde dein Ergebnis auf zwei Nachkommastellen.

Problem/Ansatz:

 8,00m

4,80m

6,40m

Comments

Figur fehlt!

Answer 1

Berechne den Umfang und den Flächeninhalt der Figur(Dreieck). Runde dein Ergebnis auf zwei Nachkommastellen.
c=8,00m
a=4,80m
b=6,40m

U=8,00m+4,80m+6,40m=19,20m

cos(α)= \( \frac{b^2+c^2-a^2}{2bc} \)

cos(α)= \( \frac{6,4^2+8^2-4,8^2}{2*6,4*8} \)=0,8

α=36,87°

cos(β)= \( \frac{4,8^2+8^2-6,4^2}{2*4,8*8} \) = 0,6

cos(β)= \( \frac{a^2+c^2-b^2}{2ac} \)

β=53,13°

γ=90°

A=\( \frac{1}{2} \)*a*b

A=\( \frac{1}{2} \)*4,8*6,4

A=15,36\( cm^{2} \)

Answer 2

Ich gehe mal von dieser Figur aus:

Der Umfang ist dann 4,8+6,4+8=19,2.

Für den Flächeninhalt eines Dreiecks mit 3 gegebenen Seiten gibt es eine Formel in der Formelsammlung (Heron'sche Formel). Man kann aber auch zuerst h berechnen als Lösung des Systems (1) h²+p²=4,8² (2) h²+q²=6,4² (3) p+q=8. Dann ist h=3,84. Dies eingesetzt in die Flächenformel A_Δ=g·h/2 ergibt A_Δ=15,36. Gerundet wird da nichts. Das macht stutzig. Wahrscheinlich ist meine Skizze falsch beschriftet.

Comments

ich glaube von Heron

Wenn du den griechischen Mathematiker nicht so genau kennst - macht nichts. Es gibt da noch einen anderen, von dem du doch bestimmt schon mal gehört hast.