Hallo Proluci,
Willkommen in der Mathelounge!
Vorwissen:
Winkelsumme des Dreiecks ist 180°
Prima, dann schreibe ich das doch mal formal hin:$$\alpha + \beta + \gamma = 180°$$und nun für \(\beta\) und \(\gamma\) die Ausdrücke aus Aufgabenteil a) einsetzen:$$\begin{aligned}\alpha + \underbrace{2\alpha}_{=\beta} + \underbrace{5\alpha}_{=\gamma} &= 180° \\ 8\alpha &= 180° &&|\, \div 8 \\ \alpha &= 22,5°\end{aligned}$$Im Bild sieht das so aus:
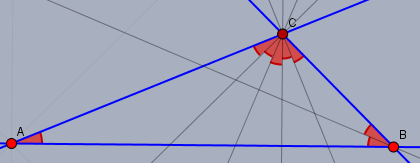
alle rot markierten Winkel sind gleiche groß. \(\beta\) und \(\gamma\) kannst Du nun selber berechnen - oder?
c) β = α + 25% und γ = α + 35%
statt \(x+ 25%\) kann man auch schreiben: \(x \cdot \left( 1 + \frac{25}{100}\right) = x\cdot 1,25\). Folglich gilt hier:$$\begin{aligned}\alpha + \underbrace{(\alpha + 25\%)}_{ß} + \underbrace{(\alpha + 35\%)}_{\gamma} &= 180° \\ \alpha + 1,25 \alpha + 1,35\alpha &= 180°\\ 3,6\alpha &= 180° &&|\, \div 3,6 \\ \alpha &= 50° \\ \implies \beta &= 1,25 \cdot 50° = 62,5° \\ \gamma &= 1,35 \cdot 50° = 67,5°\end{aligned}$$
e) β ist 50% von α und γ ist 30% von α
"50% von etwas" ist die Hälfte - also: \(\beta = 0,5\alpha\) und "30% von etwas" sind \(30/100\)'stel von etwas - also \(\gamma = 30 \alpha / 100 = 0,3\alpha\). Wenn Du noch Fragen hast, so melde Dich bitte.