Lineare Gleichungen zwei Kreise

Question

Aufgabe:

Zwei Kreise berühen sich. Sie haben gemeinsame Tangente t. r=4,5 cm . Gesucht R. Aufgabe soll ducht lineale Gleichung gelöst werden.

Problem/Ansatz:

Answer 1

Hallo,

Für das Dreieck \(M_1PM_2\) gilt

$$\begin{aligned}(r+R)^2 &= 12^2 + (R-r)^2 \\ \implies R &= \frac{12^2}{4r} = 8\end{aligned}$$

Comments

Vielen Dank!

Gibt es den Weg ohne Pythagoras?

---

Gibt es den Weg ohne Pythagoras?

Ja - über ähnliche Dreiecke:

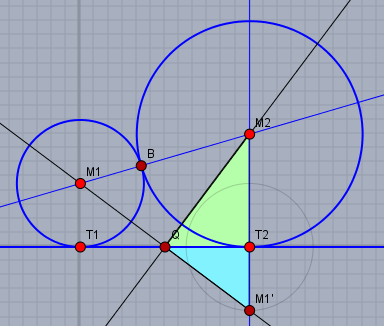
Füge einen Punkt \(M_1'\) hinzu, der sich im Abstand \(r\) unterhalb der gemeinsamen Tangenten unter \(T_2\) befindet. Der Mittelpunkt \(Q\) der Strecke \(M_1M_1'\) liegt auf der gemeinsamen Tangenten und halbiert die Strecke \(T_1T_2\) (s.Bild) 

Die Mittelsenkrechte von \(M_1M_1'\) geht durch \(M_2\), da \(|M_1M_2| = |M_1'M_2|\). Die Dreiecke \(\triangle QT_2M_2\) und \(\triangle QM_1'T_2\) sind ähnlich. Folglich gilt:$$\frac{R}{\frac{12}2} = \frac{\frac{12}2}{r}$$

---

Danke für die schnelle Antwort!

---

Aufgabe soll ducht lineale Gleichung gelöst werden.

Die "lineare" Gleichung ist in jedem Fal dieselbe:$$rR = \left( \frac a2\right)^2$$wenn \(a\) die oben bezeichnete Strecke von 12cm ist.

Und diese Gleichung kann man auch unmittelbar aus folgender Zeichnung ablesen:

es ist der Höhensatz im Dreieck \(M_1QM_2\). Dazu mus man natürlich begründen, dass \(|BQ|\) halb so lang wie \(|T_1T_2|\) ist, \(BQ\) senkrecht auf \(M_1M_2\) steht und der Winkel \(\angle M_2QM_1\) ein rechter ist.