Extremalproblem berechnung maximalen Fläche

Question

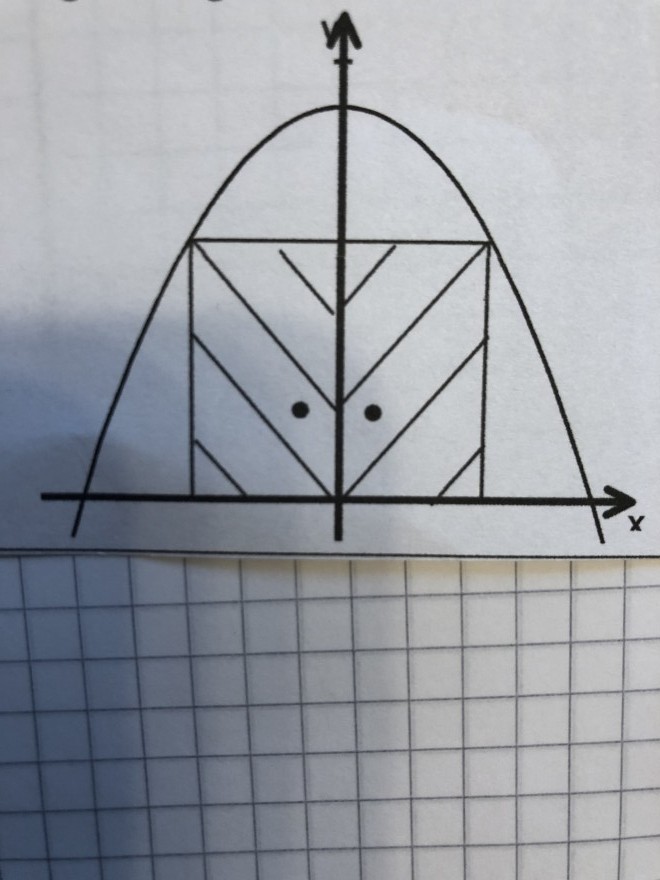
Aufgabe: Unter einem Torbogen, der durch die Funktion f(x)=-0,5x²+4,5 beschrieben werden kann, soll ein rechteckiges Tor, bestehend aus zwei rechteckigen gleich großen Torflügeln, angebracht werden. Bestimme die Maße eines Torflügels so, dass seine Fläche maximal wird. Berechne die Gesamtfläche des Tores.

Problem/Ansatz:

Ich habe leider keinen Ansatz wie ich das berechnen soll. Nur eine Skizze.

Answer 1

Die musst zunächst die Hauptbedingung und Nebenbedingung aufstellen. Die HB ist immer das, was maximal werden soll, also hier der Flächeninhalt. Hast du eine Funktionsgleichung gegeben ist diese immer die Nebenbedingung.

HB : A(x,y)= x*y

NB : y=-0,5x^2+4,5

Jetzt setzt du die NB in die HB ein. Kriegst du das hin? probier mal, wenn nicht melde dich ;)

Comments

Ich denke A(x)= x*(-0,5x²)+4,5

Wenn ja, wie würde man weitermachen?

---

Korrekt. Nun die x zusammenrechnen. Also -0,5x^3+4,5. Davon jetzt die Extremstellen berechnen.

---

Ich komme auf 0

---

Ich nicht. Wie hast du denn gerechnet?

---

Die erste Ableitung gleich null. Dabei bin ich dann auf x=0 gekommen. Bei der zweiten Ableitung -3*x also für x 0 eingesetzt, dann habe ich -3*0 gerechnet.