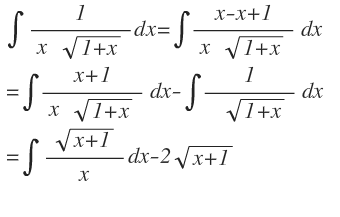
so jetzt eine nette Substitution und zwar $p=x+1$. Dann ist $dp=dx$. Nun wieder eine Null ergaenzen und dann 3. Binomische Formel im Nenner:
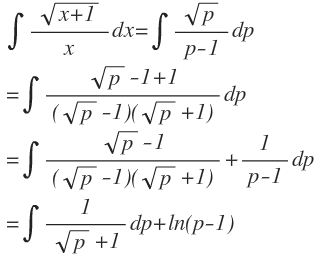
Jetzt bleibt uns nur noch $1/(\sqrt{p}+1)$ zu integrieren:
Wieder Substitution $p=y^2$, dann ist $dp=2ydy$ :
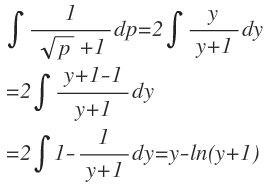
So jetzt haben wir alle Integrale ausgerechnet Nun noch ruecksubstituieren (zwei mal) und wir erhalten die Stammfunktion
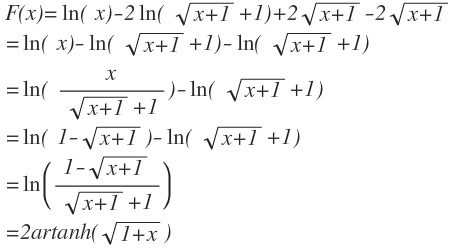
So nun die Grenzen einsetzen und man bekommt
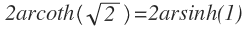
Ende.