Wo sind diese Genau Symmetrieachsen?

Question

hallo,

Wo sind diese Genau Symmetrieachsen?

Text erkannt:

Symmetrie
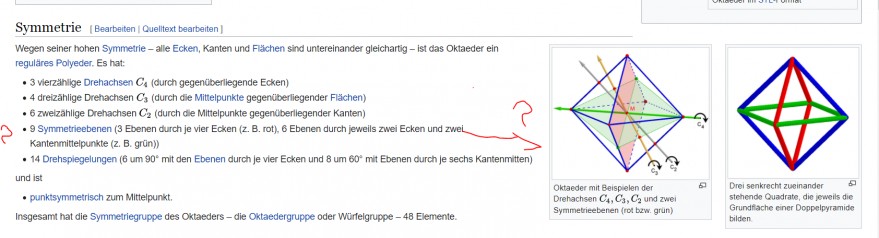
Wegen seiner hohen Symmetrie - alle Ecken, Kanten und Flächen sind untereinander gleichartig - ist das regulăres Polyeder. Es hat:
3 vierzählige Drehachsen \( C_{4} \) (durch gegenuberliegende Ecken)
- 4 dreizăhlige Drehachsen \( C_{3} \) (durch die Mittelpunkte gegeniberliegender Flächen) 6 zwelzahhlige Drehachsen \( C_{2} \) (durch die Mittelpunkte gegenuberliegender Kanten) 9 Symmetrieebenen (3 Ebenen durch je vier Ecken (z. B. rot), 6 Ebenen durch jeweils zwei Ecken und Kantenmittelpunkte (z. B. grün)) 14 Drehsplegelungen \( \left(6\right. \) um \( 90^{\circ} \) mit den Ebenen durch je vier Ecken und 8 um \( 60^{\circ} \) mit Ebenen durch je sechs Kantenmitten)
und ist Drei zum Mittelpunkt.
Insgesamt hat die Symmetriegruppe des Oktaeders - die Oktaedergruppe oder Würfelgruppe - 48 Elemente.

Comments

Was willst du denn nun genau wissen?

Answer 1

Ich habe dir zu den schon vorhandenen Drehachsen C₂, C₃, C₄ noch 3 (rot) dazugemalt.

Wo nun die Symmetrieebenen und weitere Drehachsen liegen ist schwer dazustellen, lässt sich aber ahnen.

Comments

Ich lese und melde mich später

---

schwierig immer noch