Aufgabe:
Hallo, habe bereits die Aufgaben a) und b) gelöst, aber ab Aufgabe c) komme ich nicht weiter. Auf dem Bild sind die richtigen Lösungen, allerdings wüsste ich gern die Rechenwege. Wäre sehr dankbar, wenn mir jemand die Rechenwege erklären könnte?
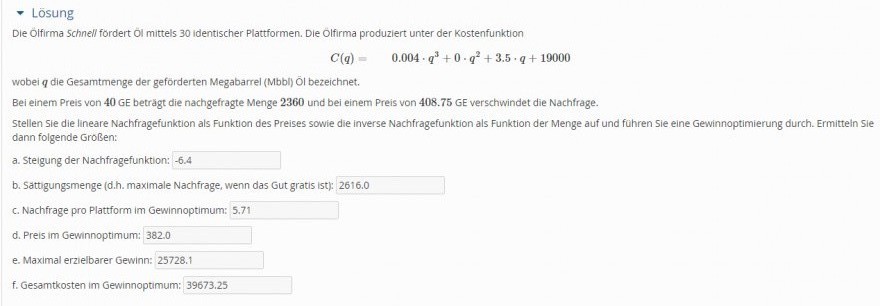
Text erkannt:
\( \boldsymbol{\sim} \) Lösung
Die Öfirma Schnell fordert ö mittels 30 identischer Plattformen. Die Olfirma produziert unter der Kostenfunktion
$$ C(q)=0.004 \cdot q^{3}+0 \cdot q^{2}+3.5 \cdot q+19000 $$
wobei \( q \) die Gesamtmenge der geförderten Megabarrel (Mbbl) Ö bezeichnet.
Bei einem Preis von 40 GE betragt die nachgefragte Menge 2360 und bei einem Preis von 408.75 GE verschwindet die Nachfrage.
Stellen Sie die lineare Nachfragefunktion als Funktion des Preises sowie die inverse Nachfragefunktion als Funktion der Menge auf und führen Sie eine Gewinnoptimierung durch. Ermitteln Sie dann folgende Großen:
a. Steigung der Nachfragefunktion: -6.4
b. Sattigungsmenge (d.h. maximale Nachfrage, wenn das Gut gratis ist): 2616.0
c. Nachfrage pro Plattform im Gewinnoptimum: 5.71
d. Preis im Gewinnoptimum: 382.0
e. Maximal erzielbarer Gewinn: 25728.1
f. Gesamtkosten im Gewinnoptimum: 39673.25