Lösung mit Rechnung:
1.) 4,5y = 9x -13,5
2.) 3y + 3x + 9 = 0
1.) 9x-4,5y -13,5 =0
2.) 3x+ 3y + 9 = 0|*3
2.) 9x+ 9y + 27 = 0
1.) 9x-4,5y -13,5 =0
2.)-1.): 13,5y+40,5=0 → y = - 3 in 2.) vereinfacht: -3 + x +3= 0 → x=0
Lösung mit Zeichnung:
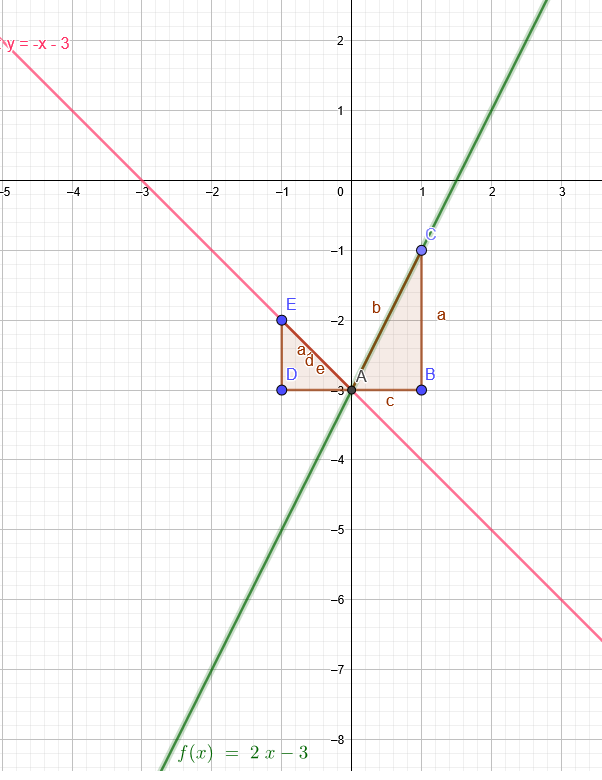
1.) 4,5y = 9x -13,5 nach y auflösen: y= 2x-3 Hier beträgt die Steigung m=2 und der y-Abschnitt n=-3
2.) 3y + 3x + 9 = 0 vereinfachen : y + x + 3 = 0 nach y auflösen: y = -x - 3 Hier beträgt die Steigung m=-1 und der y-Abschnitt n=-3
Text erkannt:
\( x \)