Rekonstruktion von Funktionen - Aufgabe Buch

Question

Aufgabe: Rekonstruktion von Funkitonen

Problem/Ansatz:

Gesucht ist eine Polynomfunktion zweiten Grades, welche die y-Achse bei y= -2,5 schneidet und einen Hochpunkt bei H (3|2) besitzt.

2. Gesucht: ganzrationale Funktion dritten Grades mit Wendepunkt W(-2|6) die an der Stelle x=-4 ein Maximum hat. Die Steigung der Wendetangente ist gleich -12

Answer 1

f(x)= ax^2+bx+c

f'(x)= 2ax+b

f(0)=-2,5

f(3)=2

f'(3)=0

c=-2,5

2=9a+3b-2,5

0=6a+b -> b=-6a

0= 9a+3(-6a)-4,5

0= 9a-18a-4,5

0=-9a-4,5

4,5=-9a

a=-0,5

b=-6a -> b= 3

f(x)= -0,5x^2+3x-2,5

f(x)= ax^3+bx^2+cx+d

f'(x)= 3ax^2+2bx+c

f''(x)= 6ax+2b

f(-2)=6

f'(-4)=0

f'(-2)=-12

f''(-2)=0

6= -8a+4b-2c+d

0=48a-8b+c

-12=12a-4b+c

0=-12a-4b

jetzt noch das Gleichungssystem lösen...das kriegst du hin :-)

Answer 2

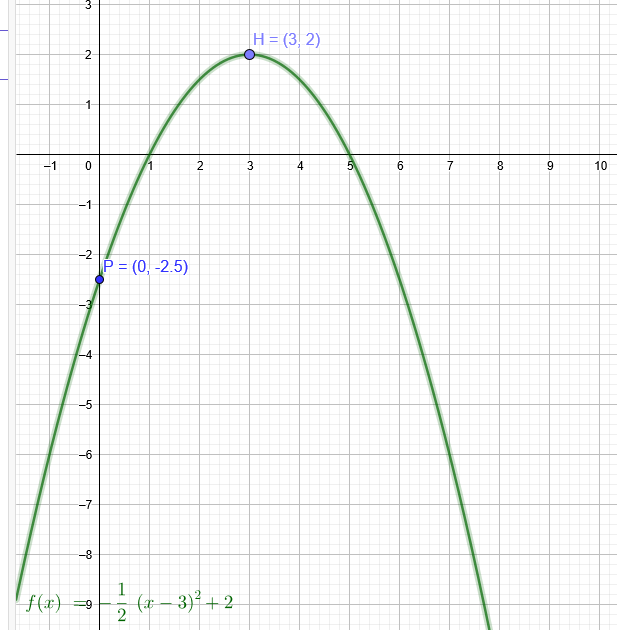
"Gesucht ist eine Polynomfunktion zweiten Grades, welche die y-Achse bei y= -2,5 schneidet und einen Hochpunkt bei H (3|2) besitzt."

Ich verschiebe den Graphen um 2 Einheiten nach unten: H´(3|0)  → doppelte Nullstelle   und Schnittpunkt bei P´(0|-4,5)

f(x)=a*(x-3)^2

P(0|-4,5)

f(0)=a*(0-3)^2

a*(0-3)^2=-4,5   a=-\( \frac{1}{2} \)

f(x)=-\( \frac{1}{2} \)*(x-3)^2

Gesuchte Parabel:

p(x)=-\( \frac{1}{2} \)*(x-3)^2+2