9)
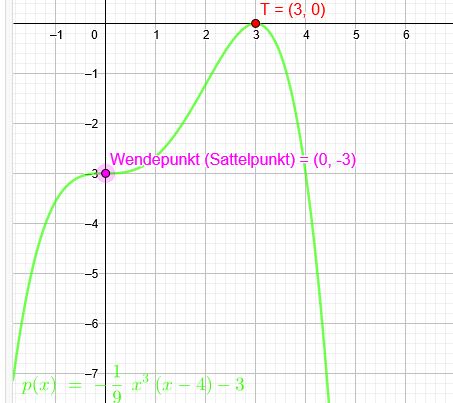
Der Graph einer ganzrationalen Funktion 4. Grades hat in \(W(0 | - 3)\) einen Wendepunkt mit waagerechter Tangente und berührt die x-Achse in \(T(3 | 0)\).
\(W(0 | - 3)\) → \(W´(0 | 0)\) ( ist eine dreifache Nullstelle):
\(f(x)=ax^3(x-N)\)
\(T(3 | 0)\) → \(T´(3 | 3)\):
\(f(3)=27a(3-N)\) \(27a(3-N)=3\) \(a=\frac{1}{27-9N}\)
\(f(x)=\frac{1}{27-9N}[x^3(x-N)]\)
\(f'(x)=\frac{1}{27-9N}[3x^2(x-N)+x^3]\)
\(f'(3)=\frac{1}{27-9N}[27(3-N)+27]=\frac{27}{27-9N}[(4-N)]\)
\(\frac{27}{27-9N}[(4-N)]=0\) \(N=4\) \(a=-\frac{1}{9}\)
\(f(x)=-\frac{1}{9}x^3(x-4)\)
3 Einheiten nach unten:
\(p(x)=-\frac{1}{9}x^3(x-4)-3\)
\(T(3 | 0)\) ist kein Tiefpunkt!