Kugel, was sagt mir diese Formel?

Question

Aufgabe:

Kugel, was sagt mir diese Formel?

Problem/Ansatz:

f(x)= Wurzel aus: r^2 - x^2 ?

Answer 1

Das sieht eher nach Kreisgleichung aus als nach Kugel.

Answer 2

Das ist die Kreisgleichung. Lässt man einen Kreis rotieren, entsteht eine Kugel.

https://www.matheretter.de/wiki/kugel

Comments

Oder ein Torus. Oder etwas dazwischen. Oder wieder derselbe Kreis. Oder noch was anderes. Es kommt halt darauf an, wo die Rotationsachse ist.

Answer 3

Der Halbkreis:   f(x) = \( \sqrt{9-x^2} \)  schaut so aus:

Comments

Liegt die immer an der x-Achse an? Und wenn das eine Funktion darstellt, dann müsste sie doch auch nach dem Schneiden der x-Achse weiterlaufen und dann länger werden und im Endeffekt keinen Halbkreis mehr zeigen oder?

---

In der Form f(x)=\( \sqrt{r^2-x^2} \) liegt sie immer an der x-Achse an.

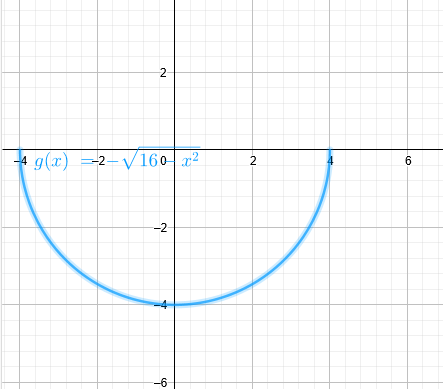
Im Vergleich dazu g(x)=- sqrt(16-x^2):diese liegt auch an der x-Achse an, aber von unten  her.

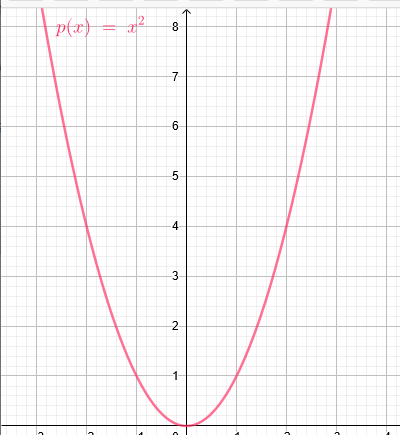
Bei einer Funktion wird dem x-Wert immer nur ein y-Wert zugeordnet. z.B. p(x)=x^2

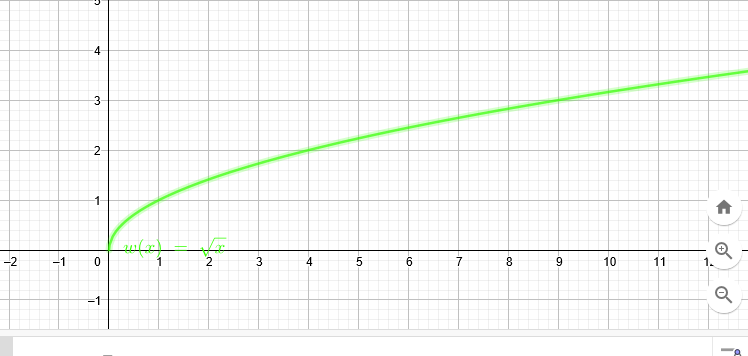
Bei der Funktion w(x)= \( \sqrt{x} \)  hast du auch nur einen Teil , der der x-Achse anliegt.

Die verschiedenen Farben tauchen wieder in den Graphen auf: