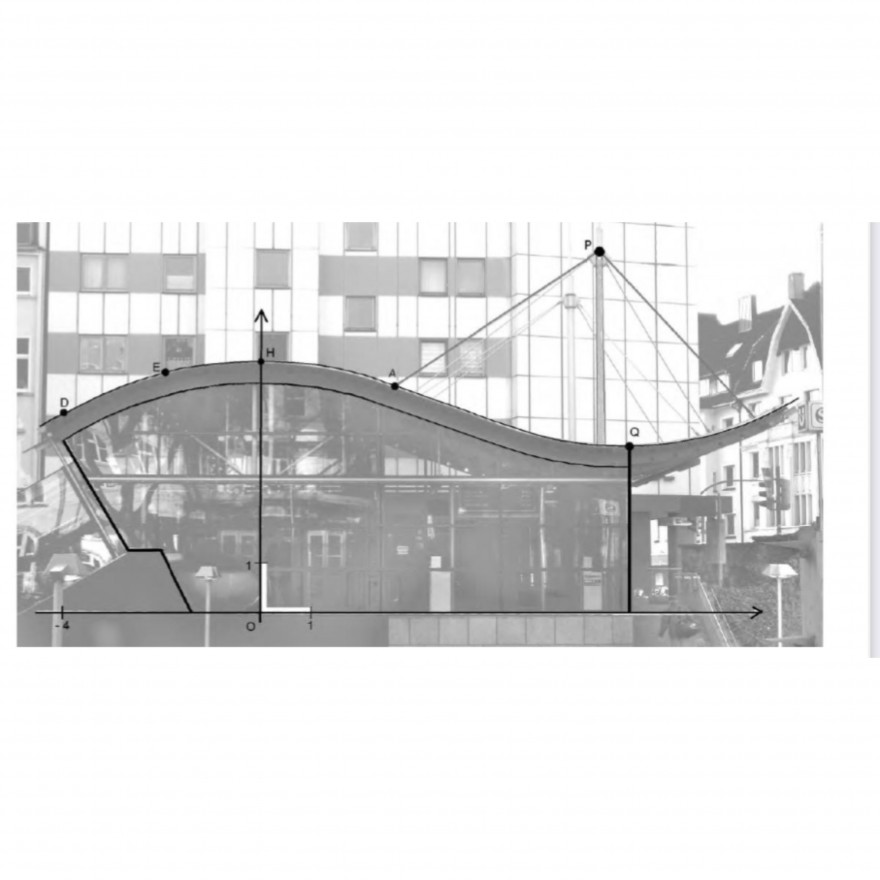
Aufgabe:Die Abbildung zeigt das Eingangsgebäude zu einer U-Bahn-Haltestelle. Auf dem Foto schaut man frontal auf eine ebene Glasfläche, die sich unter einem geschwungenen Dach befindet.
Die Dachoberkante wird durch die Funktion h modelliert: h(x)=0,0004x^4+0,0016x^2+5 Eine Längeneinheit in dem eingezeichneten Koordinatensystem entspricht 1 m.
Der höchste Punkt der Dachoberkante befindet sich in diesem Koordinatensystem bei (0|h(0)).
Der tiefste Punkt liegt bei (7,5|h(7,5)).
Auch die Punkte (−4|h(−4)) und (−2|h(−2)) liegen auf der Dachoberkante. Der Punkt hat eine Höhe von 4,59

Text erkannt:
e) Berechnen Sie die mittlere Steigung der Dachoberkante zwischen den Punkten \( D \) und \( E \). [Differenzenquotient]
f) Berechnen Sie die Punktsteigungen der Dachoberkante in den Punkten \( E, H \) und \( A \). [Setzen Sie die \( x \) -Werte in \( h^{\prime} \) ein.]
Oberhalb des Daches sind verschiedene geradlinig verlaufende Stahlseile angebracht. Ein Stahlseil verläuft von \( A \) nach \( P(6,7 \mid 7,2) \).
g) Ermitteln Sie die Funktionsgleichung der linearen Funktion \( g \), deren Graph durch \( A \) und \( P \) verläuft.