Wie berechnet man aufgabe

Question

Text erkannt:

Berechnungen an geometrischen Fi
Eine kegelförmige Schultüte ist \( 50,5 \mathrm{~cm} \) lang. Die Öffnung hat einen Durchmesser von \( 15 \mathrm{~cm} \). Ermittle, wie viel Quadratmeter Folie zum Bekleben benötigt werden. Q
Die Abbildung zeigt einen zusammengesetzten Körper. Berechne, wie hoch beide Körper zusammen sind. Q Ermittle die Länge der Mantellinie des Kegels und die Größe des Winkels an der Spitze. Entscheide und begründe, welches Volumen beide Körper zusammen haben. Berononononono

Aufgabe:

Comments

Nur die aufgabe mit der schultüte bitte

---

Aufgabe 2, 3.a), 3.b) oder 3.c)?

---

Die aufgabe nummer 12 brauche ich nur

Also die kegelförmige schultüte

Answer 1

Hallo

der Umfang der Öffnung ist ein Teil des Umfangs eines Kreises mit Radius 50,5 cm. Daraus kannst du die Fläche bestimmen, denn sie ist derselbe Bruchteil der Fäche des Kreises mit denn 50,5cm Radius

Gruß lul

Comments

Aber wie berechnet man das und wie viel folie braucht man dann?

---

Hallo

der Umfang  des Rands der Schultüte ist u=pi*15cm. der Umfang des Kreises, aus dem ausgeschnitten wurde ist U= pi*2*50,5cm. das Verhältnis u/U ausrechnen, dann denselben Bruchteil von der Fläche des Kreises  also von pi*50,5^2cm^2 nehmen also Fläche =u/U*pi*50,5^2cm^2

lul

Answer 2

Du kannst auch über die Formel zur Mantelfläche eines Kegels gehen. Es ist ja die Höhe und der Radius gegeben, daraus kannst du mit Pythagoras die Seitenlänge ermitteln.

Und dann M=pi*r*s...r=Radius, s=Seitenlänge

Answer 3

Hallo,

umgestülpt sieht die Tüte so aus:

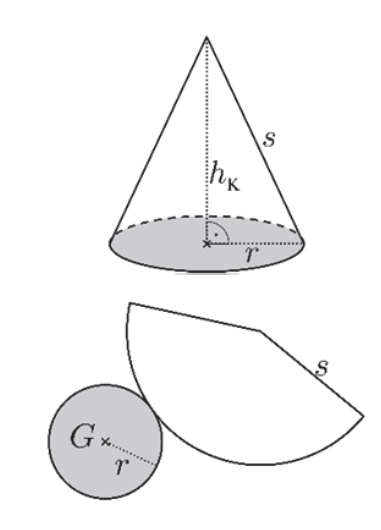
Die grauen Flächen kannst du ignorieren, weil die Tüte oben offen ist. Du musst also den Flächeninhalt der weißen Fläche = Mantelfläche berechnen.

Das machst du mit der Formel für die Mantelfläche eines Kegels \(M=\pi\cdot r\cdot s\)

s ist die Länge der Tüte, r = der halbe Durchmesser.

Gruß, Silvia

Answer 4

Hallo,

da man die Schultüte nur aussen beklebt und sie offen ist , also keinen Boden hat , benutzt man die

Formel vom Kegel, und hier die Mantelformel

M = r*s*π

gegeben ist: d= 15 cm   dann ist r = 7,5cm   h_k = 50,5 cm

nun muss man noch s ermitteln   s= \( \sqrt{r² +h²} \)

s= 51,05

alles oben einsetzen

M =1202,92cm²

weiteres auf : https://www.matheretter.de/rechner/kegel

Comments

Aber wie bekommt man denn S raus weil wenn man 7,5cm +50,5 cm rechnet bekommt man doch 106,75 raus?

---

Aber ich brauche das Ergebnis doch in Quadratmetern und nicht in cm

---

Hallo, beide Werte werden mit 2 potenziert und dann noch die Wurzel gezogen.

---

Umrechnen sollte doch nicht zu schwer sein !

---

Naja ich bin nicht so gut im umrechnen ehrlich gesagt