Question

Bei einer Pyramide mit quadratischer Grundfläche ( Seitenlänge a = 7,2 cm) beträgt der Neigungswinkel α zwischen den Seitenflächen und der Grundfläche 42°.

a) Berechne die Höhe der Pyramide.

b) Wie groß ist der Neigungswinkel β einer Seitenkante gegenüber der Grundfläche?

Answer 1

Eine kleine Skizze

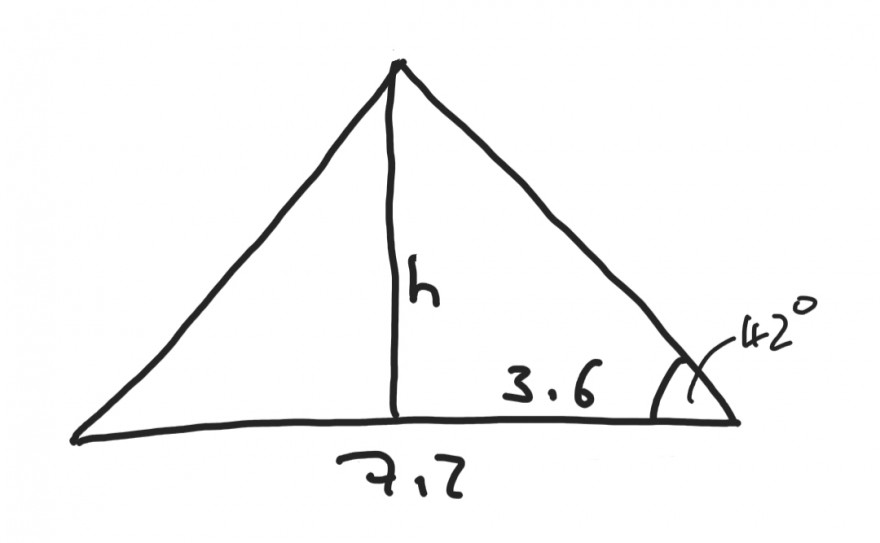
tan(42°)=h/3,6

h=tan(42°)*3,6=3,24

b) Für den Winkel der Seitenkante benötigen wir zunächst die Diagonale der Grundfläche.

D=\( \sqrt{7,2^2+7,2^2} \)=10,18

Davon nehmen wir die Häfte, weil wir die halbe Diagonale benötigen.

D/2=5,09

Jetzt basteln wir uns ein Dreieck aus der halben Diagonale, der Höhe der Pyramide und der Seitenkante und in diesem Dreieck ermitteln wir mit dem Tangens den gesuchten Winkel.

tan(β)=\( \frac{h}{\frac{D}{2}} \)

β=tan^-1(\( \frac{h}{\frac{D}{2}} \))=32,48°