Wieso wird diese Ungleichung so umgestellt?

Question

Aufgabe:

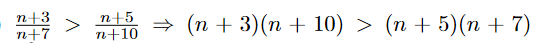
Text erkannt:

\( \frac{n+3}{n+7}>\frac{n+5}{n+10} \Rightarrow(n+3)(n+10)>(n+5)(n+7) \)

Text erkannt:

a) \( \frac{n+3}{n+7}>\frac{n+5}{n+10} \Rightarrow \)

Problem/Ansatz:

Wieso wird das so umgestellt? Wie kann aus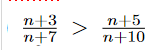

Text erkannt:

\( \frac{n+3}{n+7}>\frac{n+5}{n+10} \)

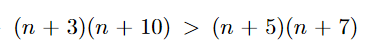folgen? Ich verstehe die Logik dahinter nicht.

Vielen Dank!

Text erkannt:

\( (n+3)(n+10)>(n+5)(n+7) \)

Answer 1

Aloha :)

Hier wurde ein Rechenschritt ausgelassen:

$$\left.\frac{n+3}{n+7}>\frac{n+5}{n+10}\quad\right|\text{Beide Brüche erweitern}$$$$\left.\frac{n+3}{n+7}\cdot\underbrace{\frac{n+10}{n+10}}_{=1}>\frac{n+5}{n+10}\cdot\underbrace{\frac{n+7}{n+7}}_{=1}\quad\right|\text{Zähler mal Zähler und Nenner mal Nenner}$$$$\left.\frac{(n+3)(n+10)}{(n+7)(n+10)}>\frac{(n+5)(n+7)}{(n+10)(n+7)}\quad\right|\text{Beide Seiten mit \((n+7)(n+10)\) multiplizieren}$$$$(n+3)(n+10)>(n+5)(n+7)$$

Das kannst du nun leicht auflösen:

$$\left.n^2+13n+30>n^2+12n+35\quad\right|-n^2$$$$\left.13n+30>12n+35\quad\right|-12n$$$$\left.n+30>35\quad\right|-30$$$$n>5$$

Answer 2

Da alle Terme für natürliche Zahlen positiv sind, ändert sich das Größer-Zeichen nicht beim Multiplizieren mit den Nennern.

Für positive Werte von a, b, c und d gilt:

\(\frac a b > \frac c d ~~~|\cdot b\cdot d\\ a\cdot d> b\cdot c\)

:-)