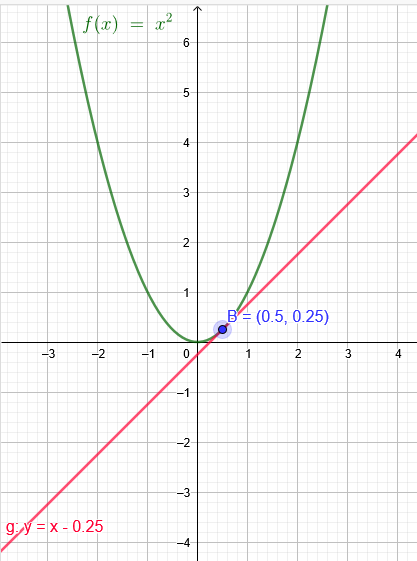
Eine Gerade mit Steigung k berührt die Parabel p. Bestimme die Geradengleichung und den Berührungspunkt
gegeben: k =1 p: y = x^2
Eine Gerade mit Steigung k:
y=k*x + b
y= 1 *x + b
berührt die Parabel y=x^2
x^2=x + b
x^2-1*x=b
(x-0,5)^2=b+0,25|\( \sqrt{} \)
1.) x-0,5=\( \sqrt{b+0,25} \)
x₁=0,5+\( \sqrt{b+0,25} \)
2.) x-0,5=-\( \sqrt{b+0,25} \)
x₂=0,5-\( \sqrt{b+0,25} \)
Bei Berührung wird +- \( \sqrt{b+0,25} \)=0→b=-0,25
Geradengleichung: y= x -0,25
Berührpunkt: B(0,5|0,25)