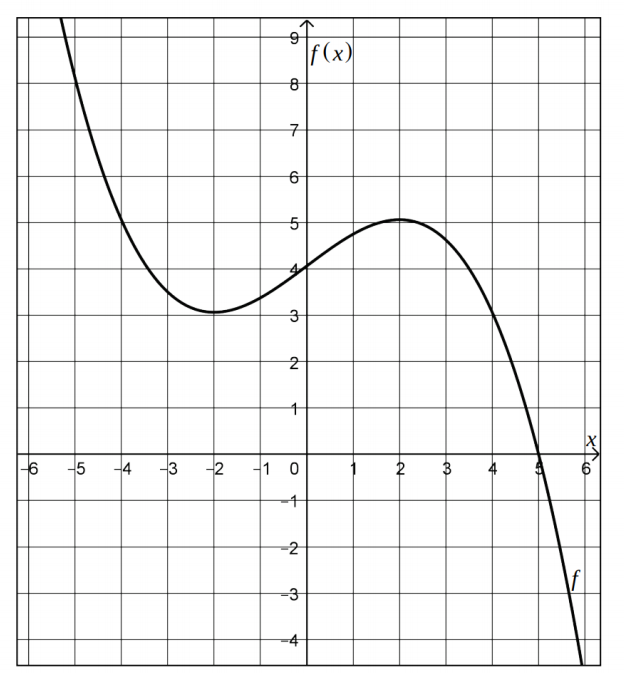
Aufgabe:
Im Bereich x=-2 bis x=2 gibt es Stellen, an denen die Tangente an den Graphen von f eine größere Steigung besitzt als die Sekante s.
Geben Sie solche Stelle an und begründen Sie Ihre Angabe mithilfe einer Rechnung.
Die Sekante verläuft durch den Tiefpunkt T(-2 / 49/16) und den Hochpunkt H (2 / 81/16).
Problem/Ansatz:
Die Steigung der Sekante ist m=0,5.
Ich habe schon eine ähnliche Aufgabe auf dieser Seite gefunden, aber konnte den Rechenweg nicht nachvollziehen.
Wie gehe ich an dieser Stelle vor?