Hallo,
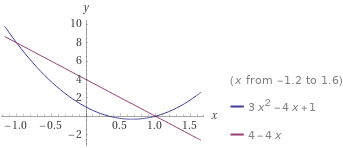
Berechnen Sie die Gleichung der Sekante, die die Funktion f (x) = 3x^2 – 4x + 1 in den Punkten P, (-1, f(-1)) und P2(1, f (1)) schneidet.
Zunächst berechne ich die beiden y-Werte:
f(-1)=3*(-1)^2-4*(-1)+1=3+4+1=8
f(+1)=3*(+1)^2-4*(+1)+1=3-4+1=0
Wir haben also die Punkte
P1(-1|8) und P2(1|0)
Die Sekante ist die Gerade, die durch die beiden Punkte verläuft. Die Geradengleichung sieht allgemein so aus:
y=m*x+b
Dabei müssen m und b mit Hilfe der beiden Punkte berechnet werden.
P1: 8=m*(-1)+b (1)
P2: 0=m*1 +b (2)
Ich subtrahiere die zweite minus die erste Gleichung, damit b wegfällt.
-8=2*m → m=-4
Das setze ich jetzt in (2) ein.
0=-4+b → b=4
y=-4x+4
:-)