Dein Kommentar ist richtig, ist aber aus der Zeichnung nicht gleich ersichtlich.
Andere Ansätze:
1.) f(x)=a*(x-14)^2+20
Startpunkt(0|0)
f(0)=a*(0-14)^2+20
a*(0-14)^2+20=0
a=-\( \frac{5}{49} \)
f(x)=-\( \frac{5}{49} \)(x-14)^2+20
Landepunkt(30|-5)
f(30)=-\( \frac{5}{49} \)(30-14)^2+20
-\( \frac{5}{49} \)(30-14)^2+20≠-5
Nun liegt der Landepunkt nicht mehr auf dem Graph.
2.) f(x)=a*x^2+b*x + c
f´(x)=2ax+b
f´(14)=2a*14+b
28a+b=0 →b=-28a
f(x)=a*x^2-28a*x + c
Startpunkt(0|0)
f(0)=a*0^2-28a*0 + c
c=0
maximale Sprunghöhe(14|20)
f(14)=a*14^2-28a*14 + 0
196a-28*a*14=20→98a-14*a*14=10→98a-196*a=10→-98a=10→a=-\( \frac{5}{49} \)
b=-28*(-\( \frac{5}{49} \))→-4*(-\( \frac{5}{7} \))
b=\( \frac{20}{7} \)
f(x)=-\( \frac{5}{49} \)*x^2+\( \frac{20}{7} \)*x
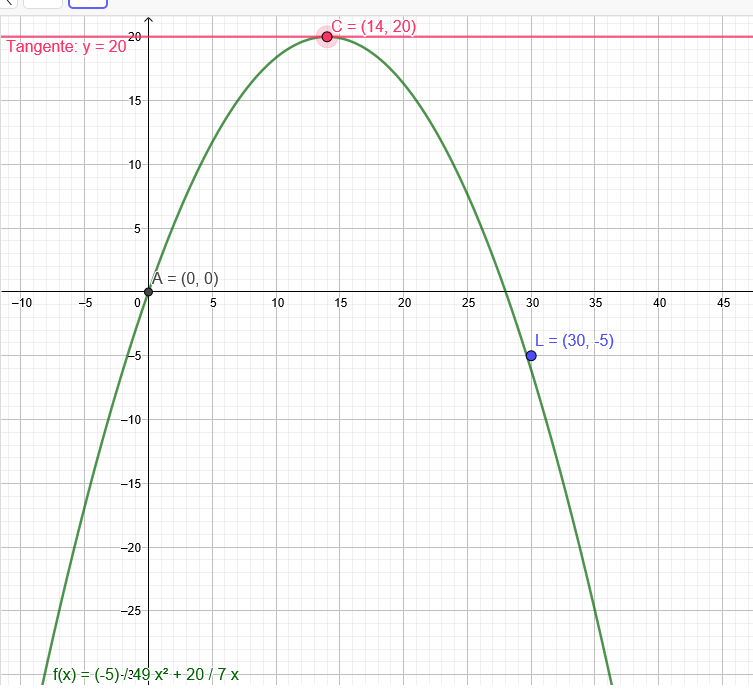
So stimmt es auch nicht! Wie lautet denn nun die ganz korrekte Funktion?