Aufgabe:
Zur Gewinnermittlung wird die Kostenfunktion K(x)=x^3-9*x^2+55*x+190 und die Erlösfunktion E(x)=90*x verwendet
Stellen sie die Funktionsgleichung der Gewinnfunktion auf und berechnen sie die Höhe des maximalen Gewinns?
Problem/Ansatz:
ohne den Preis zu wissen tue ich mir schwer und mich verwirrt wenn ich die Funktion in Geogebra eingebe kommt raus x=-2,333 - warum minus, dass ist doch die Menge oder?…
Kann das die Lösung sein:
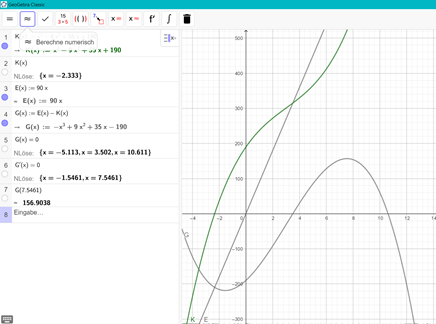
Text erkannt:
\( K(x)=x^{2}-9 x^{2}+55 x+190 \quad=1 x \)
\( \rightarrow K(x):=x^{3}-9 x^{2}+55 x+190 \)
\( \mathrm{K}[\mathrm{x}) \)
NLose: \( (x=-2.333) \)
\( E(x)=60 x \)
\( E(x)=90 x \)
\( C(x):=E(x)-\mathbb{X}(x) \)
\( G(x):=-x^{3}+9 x^{2}+35 x-190 \)
Eimgabe..