Hallo Erwin,
wenn eine Funktion \(y=f(x)\) gegeben ist, ist eine Parameterdarstellung einfach zu finden. Setze \(x=t\) und dann wird$$C(t) =\begin{pmatrix}x(t)\\ y(t)\end{pmatrix} = \begin{pmatrix}t\\ t^2-2\end{pmatrix} $$
b) Für welche Parameterwerte (t1,t2), liegt C(t1) u. C(t2) auf der horizontalen Koordinatenachse?
auf der horizontalen Koordinatenachse ist \(y=0\). Daraus folgt$$t_{1,2}^2-2 = 0 \quad \implies t_1=\sqrt{2}, \quad t_s=-\sqrt{2}$$
c) Bestimmung von C(t1) + Richtungsvektor der Tangente in diesem Punkt.
Der Richtungsvektor einer Tangente ist die Ableitung der Parameterform nach \(t\)$$\frac{\partial C}{\partial t} = \begin{pmatrix}1\\ 2t\end{pmatrix}$$Daraus folgt die Parameterform der Tangente \(g\) im Punkt \(C(t_1)\)$$g: \quad \vec x = C(t_1) + \frac{\partial C(t_1)}{\partial t} \mu \\ \phantom{g: \quad \vec x }= \begin{pmatrix}\sqrt{2}\\ 0\end{pmatrix} + \begin{pmatrix}1\\ 2\sqrt{2} \end{pmatrix} \mu$$
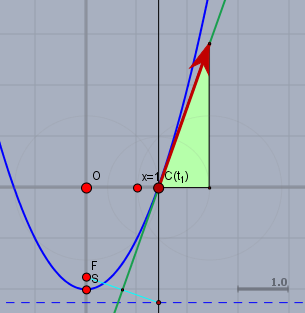
das Bild bestätigt die Rechnung.
Gruß Werner