Warum ist eine Exponentialfunktion durch zwei Punkte eindeutig bestimmt?

Question

Aufgabe:

Weshalb ist eine Exponentialfunktion in Form von a·b^{x} durch zwei gegebene Punkte eindeutig bestimmbar?

Was meinen die? Bitte erklärt mir das einfach ohne diesen Parameter. Ich kenne nur diese Formel: f(x) = c·a^{x}

Comments

Die Aufgabenstellung sollte statt  "Weshalb eine Exponentialfunktion ..."  besser  "Wann eine Exponentialfunktion ..."  heißen.

Answer 1

 

wenn eine Exponentialfunktion allgemein durch die von Dir angegebene Formel

f(x) = c * a^x

beschrieben wird, fehlen uns ja nur die beiden Parameter c und a, um die Funktion eindeutig zu bestimmen.

Und wenn wir 2 Punkte gegeben haben, erhalten wir letztlich 2 Gleichungen mit 2 Unbekannten, die wir einfach lösen können.

 

Beispiel:

Gegeben die beiden Punkte A(0|5) und B(1|6)

Wir setzen ein

f(0) = 5 = c * a⁰ = c

f(1) = 6 = c * a¹

Also

5 = c

Einsetzen in 6 = c * a¹ liefert uns das a:

6 = 5 * a | a = 6/5 = 1,2

 

Damit lautet die gesuchte Exponentialfunktion

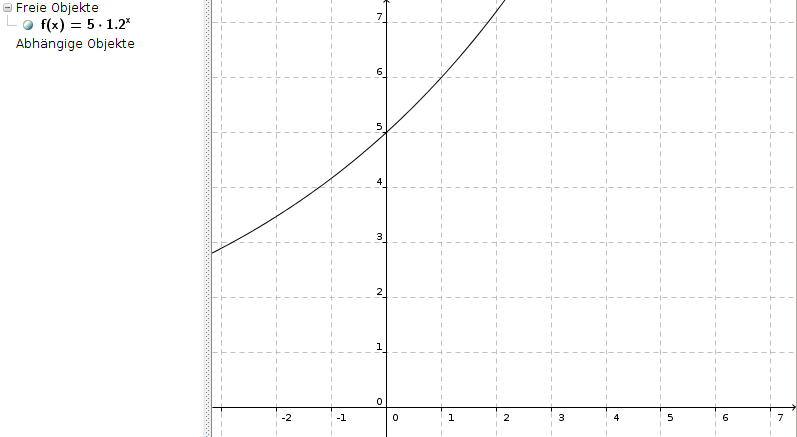
f(x) = 5 * 1,2^x

 

Besten Gruß

Comments

wie meine funktion ist falsch?

welche funktion muss ich anwenden?

und wie lautete jetzt ie antowrt zur frage

---

Deine Funktion

f(x) = c * a^x

ist richtig, aber es ist eben nur eine allgemeine Funktionsgleichung.

In dem Moment, wo man zwei konkrete Werte (Punkte) einsetzt, erhält man die spezielle Funktionsgleichung, die zu diesen beiden Punkten passt!

(Dann stehen auch nicht mehr c und a da, sondern für diese beiden Parameter ganz bestimmte Werte.)

Die Antwort auf Deine Frage habe ich oben gegeben:

Wenn man 2 Punkte in die allgemeine Funktionsgleichung einer Exponentialfunktion einsetzt, erhält man die spezielle Exponentialfunktion, auf derem Graph diese beiden Punkte liegen.