Natürlich darfst du fragen, aber die Lösung dieser Augabe wird dich wahrscheinlich nicht befähigen, andere Aufgaben zu lösen, denn Parabel-Aufgaben gibt es wie Sand am Meer.
a) Zeige, dass die Position von Peter im Koordinatensystem die Stelle x=-6,9 ist.
Hier sind die Nullstellen der Funktion zu berechnen.
b) Berechne, die Flugweite der Dose
= Abstand zwischen den Nullstellen
c) Berechne, mit wie viel Abstand die Dose das Hindernis überfliegt.
3m von Peter entfernt heißt x = -6,9 + 3 = -3,9
Berechnet f(-3,9) und die Differenz zu 0,5.
d) Berechne den höchsten Punkt in der Flugbahn der Dose
Ich weiß nicht, ob ihr schon Ableitungen hattet oder die Normal- in die Scheitelpunktform umwandeln sollt.
Der Scheitelpunkt hat die Koordinaten s (-2 | 1,2)
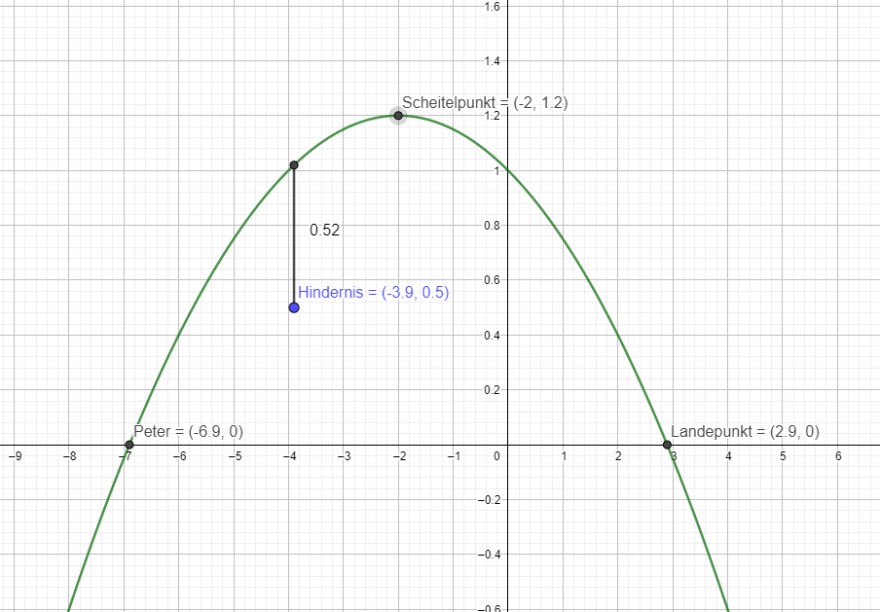
Graphisch sieht das Ganze so aus: