Lösung der Sinus-Gleichung sin(x)*84+sin(2x)*84=114,75

Question

Hi,

ich hab hier eine Gelichung und irgendwie komm ich nicht drauf wie man sie löst.

sin(30)*84+sin(60)*84=114,75

logisch

auch schreibbar als

sin(30)*84+sin(2*30)*84=114,75

immernoch logisch und einfach

jetzt aber 30 grad durch x ersetzt

sin(x)*84+sin(2x)*84=114,75

wie errechne ich jetzt x ?

Comments

Du hast es hier mit einer sog. trigonometrischen Gleichung zu tun.

Es ist nicht von vornherein sicher, dass solche Gleichungen mit normalen Umformungen lösbar sind.

Du kannst aber erst mal die 84 ausklammern und durch 84 dividieren.

Dann helfen oft die Doppelwinkelformel und der Pythagoras ein Stück weiter.

Ein Zusammenstellung solcher Formeln hat's hier:

https://www.mathelounge.de/8353/zeigen-dass-alle-reellen-zahlen-gilt-sin-cos-cos-cos²x-sin²x

Wenn du auflösen willst, sorgst du erst mal dafür, dass nur noch ein Argument vorkommt. Also hier nur x nicht noch 2x  im sog. Argument der Winkelfunktion(en). Dann möglichst nur noch eine Winkelfunktion. Manchmal kann man irgendwann sin x durch u substituieren und dann eine quadratische Gleichung erst mal nach u auflösen.

Answer 1

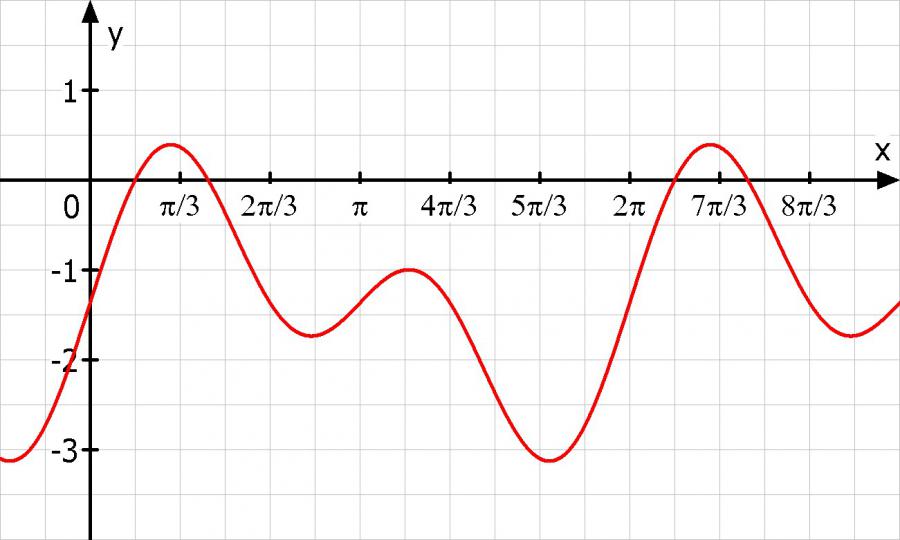
Das würde z.B. mit dem Newtonverfahren gehen

84·sin(2·x) + 84·sin(x) = 114.75

f(x) = sin(2·x) + sin(x) - 153/112 = 0

x_n+1 = x_n - f(x_n) / f '(x_n)

x_n+1 = x_n - (sin(2·x_n) + sin(x_n) - 153/112) / (2·cos(2·x_n) + cos(x_n))

x₁ = 0
x₂ = 0.4553571428
x₃ = 0.5195362452
x₄ = 0.5236059070
x₅ = 0.5236234405
x₆ = 0.5236234408
x₇ = 0.5236234408 = 30.00141321 Grad

Es gibt aber noch eine weitere Lösung die wir über einen anderen Startwert erreichnen.