Für welchen Punkt P der geraden G mit der Gleichung Y =-6/5 X +4 hat das Rechteck mit O und P als Eckpunkten den …

Question

Aufgabe. Für welchen Punkt P der geraden G mit der Gleichung Y =-6/5 X +4 hat das Rechteck mit O und P als Eckpunkten den größten Flächen Inhalt ?

Problem/Ansatz: alles

Answer 1

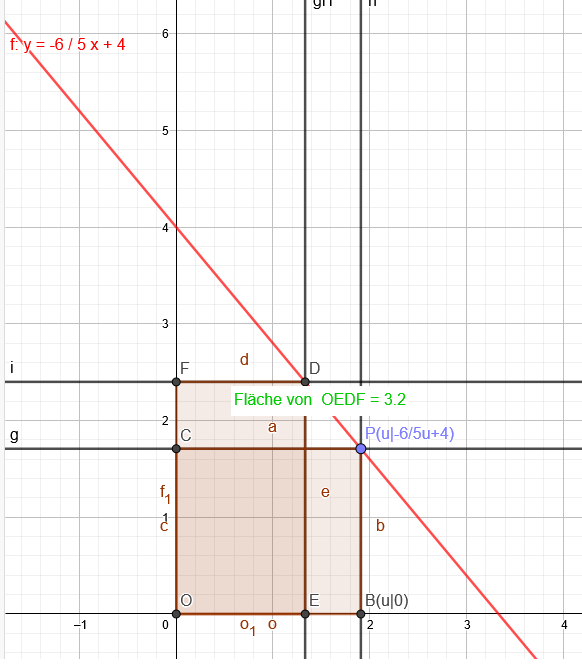
f(x)=-\( \frac{6}{5} \)x+4

P(u|f(u))

f(u)=-\( \frac{6}{5} \)u+4

A=u*f(u) soll maximal werden.

A=u*(-\( \frac{6}{5} \)u+4)

A=-\( \frac{6}{5} \)u^2+4u

A´=-\( \frac{12}{5} \)u+4

-\( \frac{12}{5} \)u+4=0

\( \frac{12}{5} \)u=4

u=\( \frac{20}{12} \)=\( \frac{4}{3} \)

f(\( \frac{4}{3} \))=-\( \frac{6}{5} \)*\( \frac{4}{3} \)+4=\( \frac{12}{5} \)

Comments

u=\( \frac{20}{12} \)=\( \frac{4}{3} \)

$$u= \frac{20}{12} = \frac{\color{red}5}3, \quad \implies f(u) = 2$$Tipp: das Optimum liegt bei diesen Typ Aufgaben immer in der Mitte. Und wenn \(f(0)=4\) ist, dann muss \(f(x_{\text{opt}})=2\) sein.

---

Ja, so kann es einem gehen, wenn man zu schnell rechnet! Dank auch für den Hinweis.