Aufgabe:
Monotonie gebr. rationale Funktion siehe Bilder
Problem/Ansatz:
- Vorgehen Monotonieverhalten so richtig?
zuerst Extrema berechnen, dann Polstellen und dann Tabelle mit Intervallen aufstellen
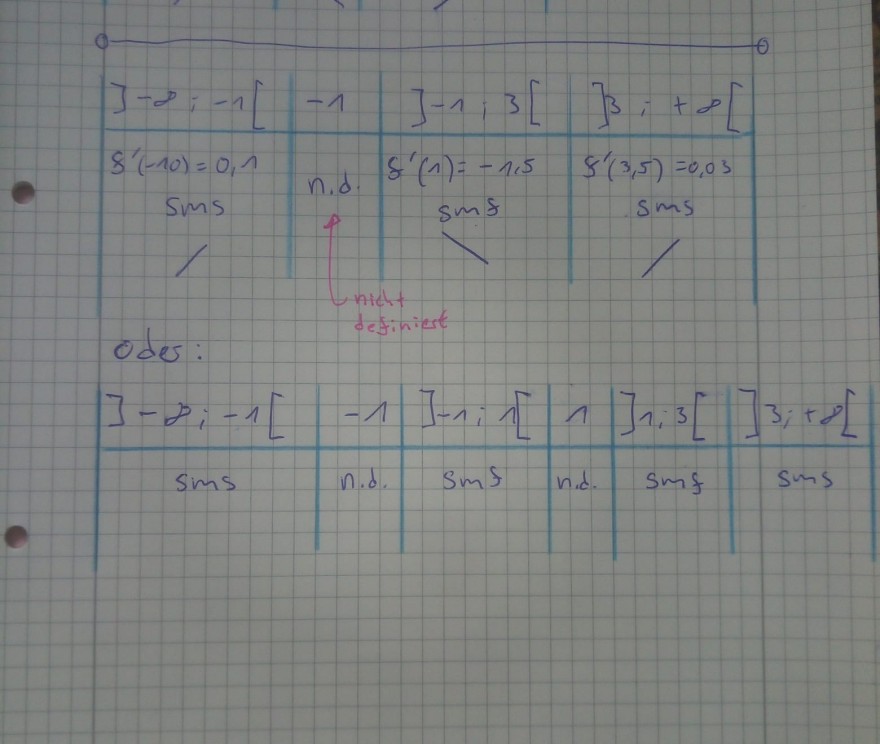
- doppelte Polstelle ja oder nein? (obere oder untere Tabelle korrekt (oder keine?))
siehe Bilder.

Text erkannt:
Nonotonie: Bed.: \( \operatorname{sms} \rightarrow f^{\prime}(x)>0 \quad S(x)=\frac{(6-6 x)}{\sin \xi \rightarrow f^{\prime}(x)<0}{(x+1)^{2}} \)
Sús dlo.otonietoselles \( z_{x+\ln a \rightarrow \text { Bed : }} \delta^{\prime}(x)=0 \)
\( f^{\prime}(x)=\frac{-6 \cdot(x+1)^{2}-(6-6 x) \cdot(2(x+1) \cdot 1)}{(x+1)^{4}} \)
\( 8^{\prime \prime}(3)=\frac{3}{32}>0 \cap \) Min bei
\( \operatorname{En}(3 /-0,75) \)
Polstelle \( \Rightarrow N(1)=0 \) \( \left.\begin{array}{l}(x+1)^{2}=0 \\ x^{2}+2 \cdot x+1^{2}=0 \\ \frac{-2 \pm \sqrt{4-4 \cdot 1 \cdot 1}}{2 \cdot 1}=x_{1 / 2}\end{array}\right\} \) odes: \( (x+1)^{2}=0 \)
\( x^{2} x=0 \)
\( x^{2}=-1 \mid \sqrt{x} \rightarrow x_{1}=-1 \)
\( x_{2}=1 \)
\( \left.\frac{-2 \pm \sqrt{0}}{2} \rightarrow x=-1 \rightarrow M=\mathbb{R} \backslash \xi-1\right\} \)
doppelte Palstelle?
\( \mid x_{5}=-1 \)
\( ? \)
\( x=1 ? \)
!