ich habe gerade meine Schwierigkeiten mit dem Thema Graphen und Zentralitätsmaße..
Erstmal eine Verständisfrage:
Ich habe folgenden einfachen, ungerichteten Graphen A:
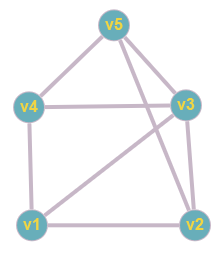
Die zugehörige Adjazenzmatrix schaut dann ja so aus (sry für die Darstellung):

Aus der kann ich ja nun erstmal nur ablesen, welchen Grad die einzelnen Knoten haben (Zeilensumme).
Wenn ich nun A² rechne, erhalte ich folgende Matrix:

Aus der kann ich nun die Anzahl der Kantenzüge der Länge 2 ablesen (1 in der Matrix).
Außerdem auf der Diagonalen den Grad der einzelnen Knoten.Richtig?
Statt A² hätte ich auch AirgendeineZahl rechnen können und könnte dann wieder auf die gleiche Art und Weise ablesen, zwischen welchen Knoten ein entsprechend langer Kantenzug besteht.
Nun die Aufgaben, bei der ich nicht so recht weiß, wie ich die angehen soll:
Sei G ein zusammenhängender, einfacher Graph mit Adjazenzmatrix A. Sei weiter B = Ak mit B = (bi,j)n,n
wobei k eine beliebige natürliche Zahl sei. Zeigen Sie, dass dann die bi,j Anzahl der Kantenzüge der Länge k zwischen vi und vj beschreibt.
Mein "Ansatz": Wenn ich das alles nicht völlig falsch verstanden habe, ist hier ja eigentlich genau das gefragt, was ich oben beschrieben habe. Nur wie schreibe ich das wieder "in mathematisch" ? :-D
2. Aufgabe bei der ich nicht weiterkomme:
Berechnen Sie die Closeness-Zentralitäten für alle Ecken/Knoten des Graphen.
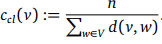
Außerdem soll ich noch die Eigenvektor-Zentralität berechnen.
Beide Begriffe tauchen in meinem Mathebuch nicht auf und selbst die Informationen die Google zu beiden Begriffen liefert sind ziemlich dünn.. :(
Könnte mir das evtl jemand anhand des obigen Graphens an einem Knoten zeigen?
Würde mich freuen, wenn mir jemand weiterhelfen könnte!