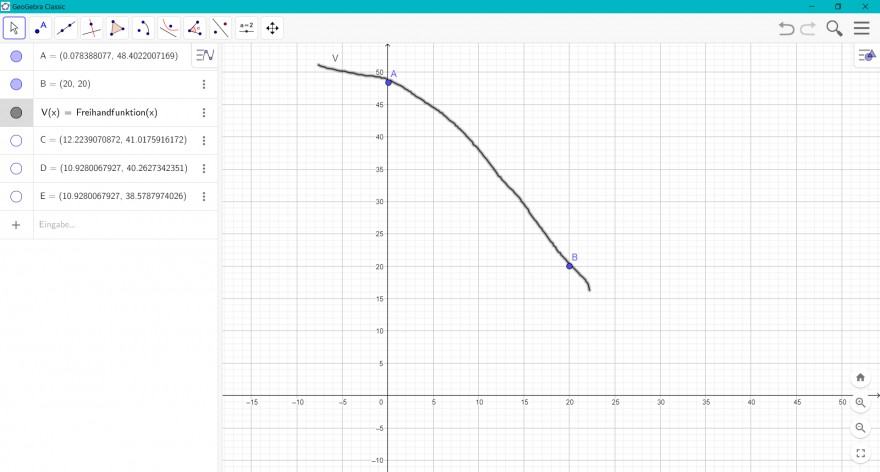
Aufgabe: Hab ich gezeichnet, weil ich nicht weiß wie ich es mit Geogebra zeichne und soll eine Heizkurve für Außentemperatur von -15 - +20 Grad darstellen:
Waagrechte Achse ist die Außentemperatur und senkrecht ist die Vorlauftempereratur V(x)
Text erkannt:
8ut \( 0 \therefore \) \( Q \)
\( 4022007169) \quad \Xi N \)
(20,
Kreuzen Sie die auf die Funktion V im Intervall (0;20) zutreffende Aussage an:
V(x) >0 und V'(x) >0
V'(x) >0 und V''(x) <0
V(x) < 0 und V''(x) <0
V'(x) <0 und V''(x) <0
V(x) <0 und V''(x) >0
Problem/Ansatz:
Ich habe ehrlich gesagt gar keinen Ansatz, ausser dass ich weiß das V'(x) eine Steigung ist und V''(x) eine Krümmung. Ich würde auch das Ergebnis, dass ich eh habe, gerne verstehen um es bei anderen Aufgaben lösen zu können. Z.B. auch wie V(x) ist also > oder > oder > und > und = 0. Eine Krümmung sehe ich z. B auch nicht, warum kommt es dann in der Antwort vor usw.