Fläche einer FKT zum Graphen berechnen

Question

Aufgabe:

Gegeben sei die Funktion f:R∖{0}⟶R
mit f(x)=(−x^2+11x−18)/(x^2)
A sei die Größe der Fläche, die vom Graph der Funktion und der x
-Achse begrenzt wird.

Problem/Ansatz:

Wie berechne ich hier die Fläche.

Bin für jede Hilfe dankbar

Comments

Kommt da vlt. ein x^3 vor.

2-mal x^2 macht wenig Sinn bzw. ist unüblich.

---

f(x)=−x2+11x−18x2

f(x)=...?

 

---

oh da ist die formatierung verutscht
habe es angepasst

Answer 1

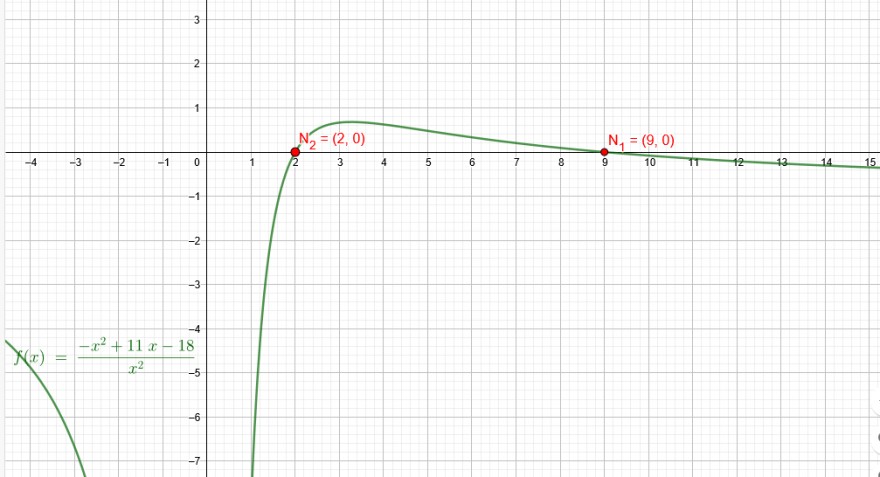
f(x)=\( \frac{−x^2+11x−18}{x^2} \)

Nullstellen:

−x^2+11x−18=0|*(-1)

x^2-11x=-18

(x-\( \frac{11}{2} \) )^2=-18+\( \frac{121}{4} \)=\( \frac{49}{4} \)|\( \sqrt{} \)

1.)x-\( \frac{11}{2} \)=\( \frac{7}{2} \)

x₁=9

2.)x-\( \frac{11}{2} \)=-\( \frac{7}{2} \)

x₂=2

\( A=\int \limits_{2}^{9} \frac{-x^{2}+11 x-18}{x^{2}} \cdot d x=\int \limits_{2}^{9}\left(-1+\frac{11}{x}-18 \cdot x^{-2}\right) \cdot d x=\left[-x+11 \ln (x)+\frac{18}{x}\right]_{2}^{9}= \)

\( =\left[-9+11 \ln (9)+\frac{18}{9}\right]-\left[-2+11 \ln (2)+\frac{18}{2}\right] \approx 2,545 F E \)