Aufgabe - Schwerpunkt eines Kegelstumpfs berechnen - Dreifachintegrale:
Wir betrachten einen Kegelstumpf mit inhomoger Dichteverteilung in dimensionsbehafteten Größen (SI-Einheiten).
Die Grundfläche des Kegelstumpfs hat den Radius \( r_{1}=0,027 \mathrm{~m} \) und liegt in der \( x y \)-Ebene. Die obere Fläche liegt in einer Höhe \( h=0,025 \mathrm{~m} \) über der Grundfläche und hat einen Radius \( r_{2}=0,012 \mathrm{~m} \)
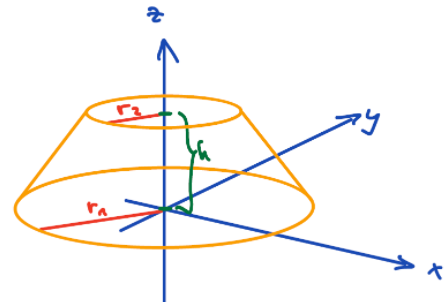
Die Dichteverteilung in diesem Kegelstumpf ist durch die Funktion gegeben:
\( \rho(\vec{r})=1,7 \frac{\mathrm{kg}}{\mathrm{cm}^{3}}+1,5 \frac{\mathrm{kg}}{\mathrm{cm}^{4}} x+0,7 \frac{\mathrm{kg}}{\mathrm{cm}^{5}} z^{2} \)
Ansatz/Problem:
Man soll die Masse dieses Kegelstumpfs berechnen - da komme ich auf 82,6523 kg, was richtig ist.
Dann muss man den Schwerpunkt bestimmen, das habe ich wie folgt gemacht:
\( \bar{x}=\int \limits_{0}^{2,5} \int \limits_{0}^{\frac{1,5 z}{-2,5}+2,7} \int \limits_{0}^{2 \pi}\left(1,7+1,5 \cos ^{4}+0,7z^{2}\right) r \cos \varphi d y \operatorname{dr} d z \)
\( \bar{x}=\int \limits_{0}^{2,5} \int^{\cdots 1} 4,71239 \mathrm{r}^{2} r dr dz = \frac{55,3707}{82,6523} = 0,66992 \)
Am Ende steht das Ergebnis der Integration durch die berechnete Masse.
So bin ich auf 0,66992 gekommen - richtige Antwort ist aber 1,19...
Ich glaube, dass ich in der faschen Reihenfolge integriere (dh. die Integranten sollten vertauscht sein), ich kann mir aber nicht erklären, wieso ich für die Masse den richtigen Wert bekomme.