Was beschreibt das "m", die sog. "Steigung"?

Question

also ich weiß durchaus wie man eine Steigung berechnet. Bei einer linearen Funktion rechnet man den Quotienten aus Delta Y und Delta X und erhält somit das Verhältnis der Werte. Aber was soll ich mir unter Steigung vorstellen?

Wenn "m", also die Steigung, gleich 5 ist, was sagt mir diese 5? Steigt die Funktion um 5 oder wie?

Ich persönlich würde eine Steigung eher mit einem Winkel definieren und nicht mit einer einfachen Zahl ohne jeglicher Einheitsangabe. Meine Lehrer konnten mir die Frage nicht beantworten, sie beeinträchtigt auch nicht meine Mathenoten, da ich ja weiß wie man eine Steigung berechnet, aber mich interessiert Mathe und ich will es verstehen und nicht nur auswendig lernen, ohne den Sinn dahinter zu kapieren.

Also was sagt mir die Steigung 5?

Comments

Man kann die Steigung m durchaus auch als Winkel ausdrücken. Das geht mit dem tangens: $$ tan \alpha =m$$

Answer 1

 

ganz einfach: Die Steigung 5 an einer bestimmten Stelle eines Funktionsgraphen sagt Dir, dass Du, wenn Du eine Stelle nach rechts gehst, um 5 Stellen nach oben gehen musst, um auf dem Graphen zu bleiben. 

Die Steigung der Funktion ist also ziemlich groß:

 

Wenn Du dagegen eine Steigung von 0,5 hast, ist die Steigung relativ klein, denn für jede Einheit, die Du nach rechts gehts, gehst Du nur eine halbe Einheit nach oben, um auf dem Graphen zu bleiben:

 

Bei einer negativen Steigung, wie zum Beispiel -2, ist der Funktionsgraph sogar nach unten gerichtet: Für jede Einheit, die Du nach rechts gehst, gehst Du 2 Einheiten nach unten:

 

Besten Gruß

Comments

danke danke :)


jetzt habe ich es verstanden...das einzige, was mich noch ein wenig verwirrt ist, denke ich jedenfalls,
das mit dem Quotienten aus Delta Y und Delta X...also das Verhältnis, aslo die 5, drückt im Prinzip aus wie oft das Delta X in Delta Y passt...oder wie? Warum genau rechnet man Delta Y durch Delta X???


danke im Voraus

---

Hello again :-)

 

warum rechnet man Delta Y/Delta X?

Weil man mit einem Steigungsdreieck rechnet. Dabei wird bestimmt, um wieviele Einheiten man "nach oben geht", wenn man eine Einheit "nach rechts geht".

Hat man zum Beispiel die Steigung 1, so geht man 1 nach rechts und 1 nach oben, das heißt 1/1 = 100%

 

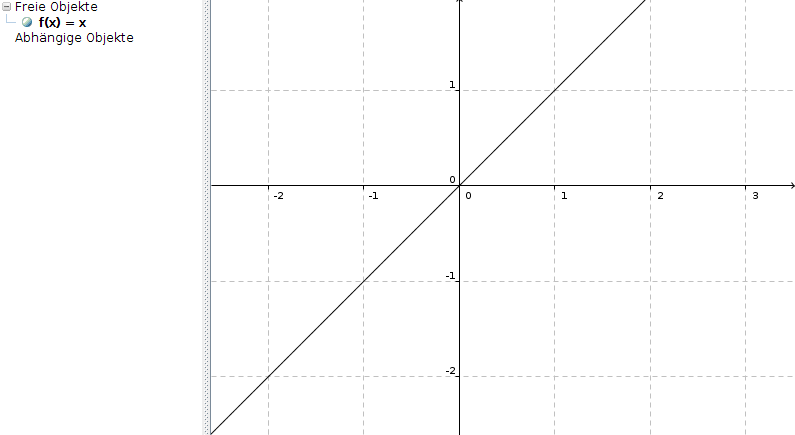
Bei einer Steigung von 2 geht man 1 nach rechts und 2 nach oben:

 

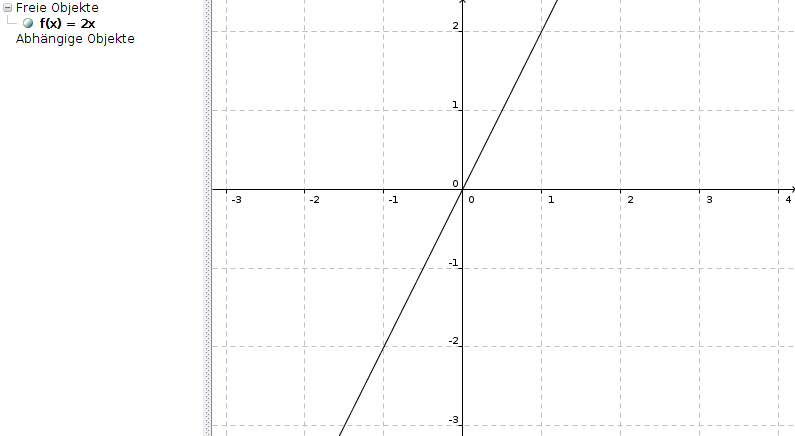
Das ist das Prinzip hinter der ganzen Sache. Da man aber nicht immer gegeben hat, um wieviel Einheiten man nach oben geht für eine Einheit nach rechts, muss man sich eben mit Delta Y/Delta X behelfen.

 

Vielleicht kann man sich dies klarer machen, wenn man sich vorstellt, dass x ein gewisses Kapital darstellt und y die Zinsen, die man in einem Jahr (wir arbeiten jetzt nicht mit Zinseszins) dafür erhält.

Bei 20% Zinsen (heutzutage absolut fantastisch) sähe die Funktion f(x) = 1,2x mit einer Steigung von 1,2 so aus:

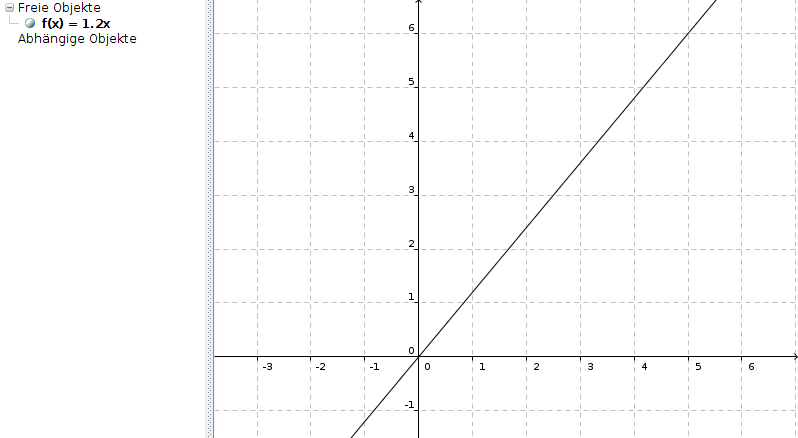
Ein Kapital von zum Beispiel 5000 Euro würde dann nach einem Jahr auf 6000 Euro anwachsen.

 

Ich hoffe, ich habe Dich jetzt nicht noch mehr verwirrt :-)

 

Falls noch etwas unklar ist, versuchen wir weiter gemeinsam, eine verständliche Erklärung zu finden.

 

Lieben Gruß

---

dankeschön jetzt ist alles klar =)

---

Sehr gut, das freut mich!

Und: Gern geschehen :-)

Answer 2

Vilelleicht versteht man es besser, wenn man statt

m = 5

schreibt:

m = 5 / 1

Dann sieht man, dass es sich bei der Steigung um ein Verhältnis handelt. Das wird ja auch durch die Formel

m = Δ y / Δx

ausgedrückt.
Indem man diese Formel ausrechnet, kürzt man den Bruch, den sie darstellt, so, dass der Nenner den Wert 1 annimmt. Somit erhält man also einen Zahlenwert, der sich auf Δ x = 1 , also auf eine Schrittweite in x - Richtung der Länge 1 bezieht.

Und dann versteht man vielleicht auch, was es bedeutet, wenn man sagt, eine Funktion habe eine Steigung von m = 5 = 5 / 1 , nämlich, dass die Funktionswerte y dieser Funktion 5 mal stärker ansteigen als die jeweiligen Argumentwerte x, dass man also für je einen Schritt in x-Richtung 5 Schritte in y-Richtung machen muss, um wieder einen Punkt auf  dem Graphen der Funktion zu erreichen.