Der Dirichlet Kern ist definiert als
$$ (1) \quad D_n(x) = \sum_{k=-n}^n e^{ikx} = 1 + 2\sum_{k=1}^n \cos(kx) = \frac{ \sin \left[ \left(n+\frac{1}{2} \right) x \right] } {\sin \left( \frac{x}{2} \right)} $$
Außerdem gibt es den Zusammenhang das die Faltung des Dirichletkerns mit einer periodischen Funktion die Fourierreihe ergibt.
D.h. es gilt
$$ (2) \quad (D_n \star f)(x) = \frac{1}{2\pi} \int_{-\pi}^\pi f(y) D_n(x-y) dy = \sum_{k=-n}^n \hat{f}(k) e^{ikx} $$
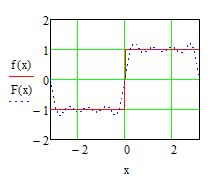
Hier ist die Funktion \( f(x) \) so definiert
$$ (3) \quad f(x)=\begin{cases} 1, & 0 \le x \le \pi \\ -1, & -\pi \le x < 0 \end{cases} $$
Einsetzen von (1) (Kosinussumme) in (2), und berücksichtigen von (3) ergibt
$$ (D_n \star f)(x) = \frac{4}{\pi} \cdot \sum_{k=1}^n \frac{1}{2k-1} \sin\left[ \left(2k-1\right) x \right] $$
Das ist die Fourierreihe für \( f(x) \)
Z.B. ergibt sich so eine Grafik, falls \( F(x) \) die Fourierreihe sein soll.