Wie berechnet man die Nullstelle der folgenden Funktion?

Question

Aufgabe:

Nullstelle der Funktion exp(x)+x

Problem/Ansatz:

Wie berechne ich die Nullstelle der folgenden Funktion?

Comments

Welcher GTR steht denn zur Verfügung?

Answer 1

Ich würde das numerisch lösen.

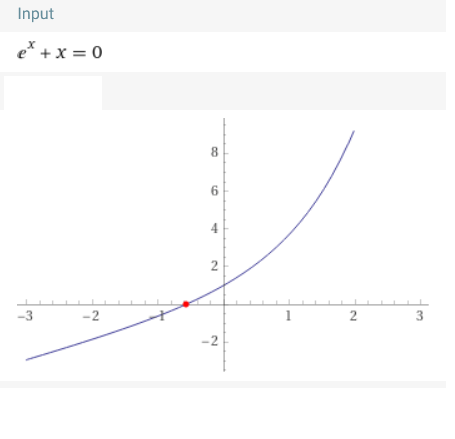
oder als

\( \frac{2}{\pi} \int \limits_{0}^{\pi} \frac{\sin \left(\frac{t}{2}\right)\left(\sin \left(\frac{3 t}{2}\right)+e^{\cos (t)} \sin \left(\frac{5 t}{2}-\sin (t)\right)\right)}{1+e^{2 \cos (t)}+2 e^{\cos (t)} \cos (t-\sin (t))} d t \)

aber das wäre Angeberei.

Answer 2

Mit einem Näherungsverfahren (Newton).

oder hiermit:

https://de.wikipedia.org/wiki/Lambertsche_W-Funktion

https://www.wolframalpha.com/input/?i=e%5Ex%2Bx%3D0

Answer 3

Algebraisch nicht zu lösen.
MIt dem Newtonverfahren
x = - 0.5671432904
Bei Bedarf : mach die Probe.