In der Aufgabe ist die Zelttür in Richtung der Y-Achse (alias \(x_2\)) geöffnet
... wenn ich das gestern schon gewusst hätte, hätte ich Dir gleich adäquat antworten können ;-)
Somit passiert alles in der YZ-Ebene. Dazu ein Schnittbild der Szene in eben dieser Ebene:
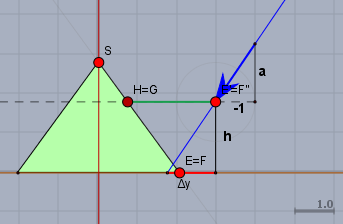
In der Skizze oben zeigt die Y-Achse nach rechts und Z wie üblich nach oben. Die blaue Halbgerade gibt den Weg eines Regentropfens an.
Es regnet genau dann in das Zelt hinein, wenn $$\Delta y \gt E'y-Ey = 2,963-2,05=0,913$$In der Skizze sind zwei ähnliche Dreiecke zu sehen, darum gilt$$\begin{aligned}\frac{\Delta y}{h} &= \frac{-1}{a} \quad h=1,8\\\implies \Delta y=-\frac{1,8}{a} &\gt 0,913&&|\,\cdot a \space (a \lt 0)\\-1,8 &\lt 0,913\,a&&|\,\div 0,913\\ \approx -1,97 &\lt a\end{aligned}$$Es regnet in das Zelt, wenn der Wert für \(a\) größer wird als \(-1,97\).
Du kannst das auch vektoriell rechnen. Stelle dazu eine Geradengleichung für den Regen auf:$$r:\quad \vec x = \begin{pmatrix}0\\ 2,936\\ 1,8\end{pmatrix} + t\begin{pmatrix}0\\ -1\\ a\end{pmatrix}$$... und berechne den Schnittpunkt mit der XY-Ebene (d.h. \(z=0\)):$$z=0 \implies 0 = 1,8 + ta \implies t = -\frac{1,8}{a}$$damit der Regen in das Zelt fällt, muss die Y-Koordinate kleiner als \(E_y\) sein:$$y = 2,963 - \frac{1,8}{a} \cdot(-1) \lt E_y = 2,05$$die Lösung ist natürlich identisch zu oben.