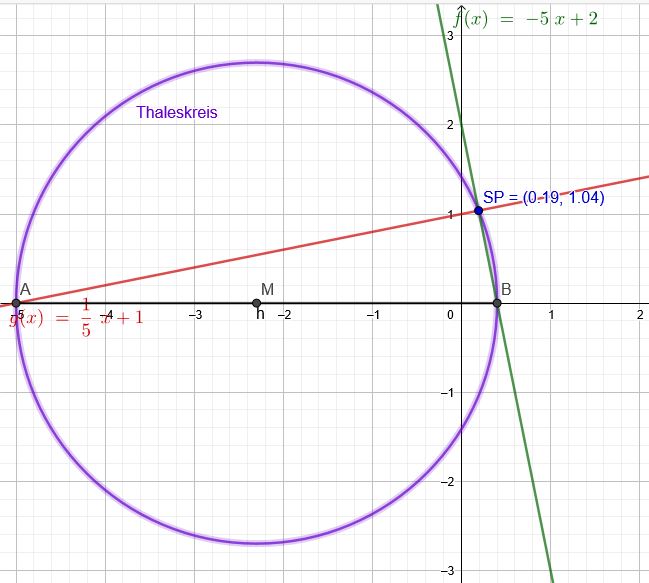
Berechne den Schnittpunkt und Schnittwinkel der Graphen von f und g c)
\(f(x)=-5x+2\) \(g(x)=\frac{1}{5}x+1\)
Schnittpunkt:
\(-5x+2=\frac{1}{5}x+1\)
\(5x+\frac{1}{5}x=1\)
\(x=\frac{5}{26}\) \(g(\frac{5}{26})=\frac{1}{5}*\frac{5}{26}+1=\frac{27}{26}\) \(SP(\frac{5}{26}|\frac{27}{26})\)
Schnittwinkel:
Allgemeine Formel:
\(tan (α)=| \frac{m_2-m_1}{1+m_1*m_2} |\)
\(m_1=-5\) \(m_2=\frac{1}{5}\)
Im Fall von \(m_1*m_2=-1\) stehen die Geraden senkrecht aufeinander:
\(-5*\frac{1}{5}=-1\) → \(α=90°\)