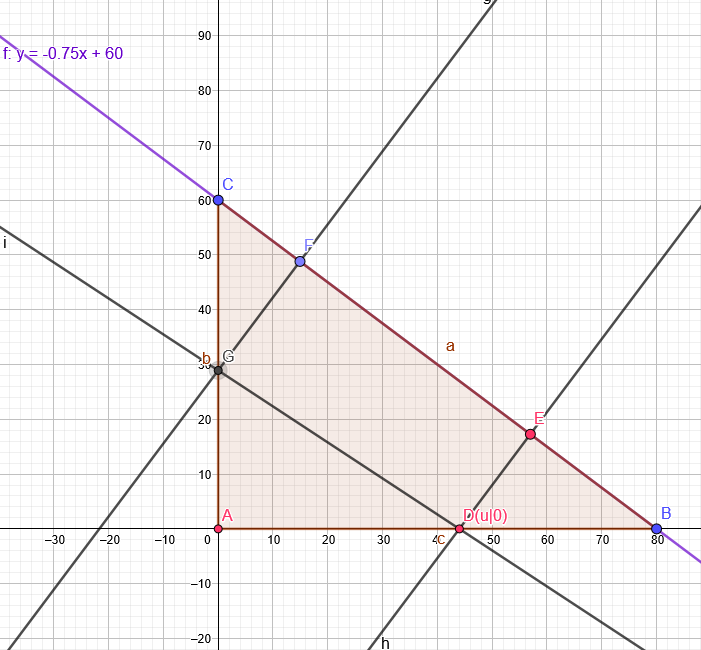
Geradengleichung durch B und C y=-0,75x+60
Geradengleichung durch D(u|0) mit m=-0,75
\( \frac{y-0}{x-u} \)=-0,75
Schnitt mit y-Achse:
\( \frac{y}{0-u} \)=-0,75
\( \frac{y}{u} \)=0,75
y=0,75u → G(0|0,75u)
Länge der Strecke D G:
l=\( \sqrt{u^2+0,75^2*u^2} \)
Gerade durch D(u|0) und E mit m=-\( \frac{1}{-0,75} \)=\( \frac{1}{0,75} \)=\( \frac{4}{3} \)
Schnitt mit y=-0,75x+60
\( \frac{y-0}{x-u} \)=\( \frac{4}{3} \)
y=\( \frac{4}{3} \)*x-\( \frac{4}{3} \)u
-0,75x+60=\( \frac{4}{3} \)*x-\( \frac{4}{3} \)u
u.s.w.