Zur Lösung eines mathematischen Problems schlug Francois Vieta 1591 eine Methode aus drei Schritten vor:
- Die bekannten wie auch die unbekannten Größen, die in dem Problem vorkommen, mit Buchstaben bezeichnen.
- Die Beziehungen zwischen diesen Größen in Gleichungen ausdrücken.
- Durch Umformungen die unbekannten Größen durch die bekannten ausdrücken.
Etwas Entsprechendes hat auch George Polya etwa 400 Jahre später vorgeschlagen und um einen weiteren Schritt ergänzt:
- Umformulierung der Aufgabe in eine gleichbedeutende und einfachere.
Vietas (bzw. Polyas) Methode soll an einem Beispiel demonstriert werden, das kürzlich in der Mathelounge erschien:
Aufgabe: Gegeben sind ein Quadrat ABCD und zwei gleichseitige Dreiecke HFC und EFG, welche die abgebildete Lage zueinander haben:
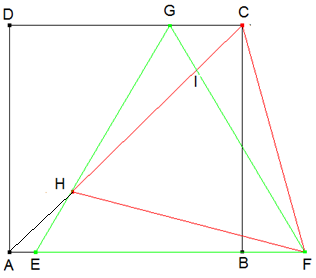
Wie verhalten sich die Flächeninhalte der Dreiecke HIG und FCI zueinander?
Hier ist es angezeigt, mit Polyas ergänzendem Schritt zu beginnen und die Aufgabe in eine gleichbedeutende, einfachere umzuformen:
Aufgabe: Gegeben sind ein Einheitsquadrat ABCD und zwei gleichseitige Dreiecke HFC und EFG, welche die abgebildete Lage zueinander haben:
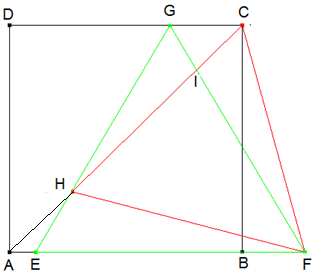
Wie verhalten sich die Längen HG und FC zueinander?
Eine Umformulierung, wie diese, setzt einige mathematische Kenntnisse voraus, wie z.B. das Wissen, dass sich ein Maßverhältnis nicht ändert, wenn man die Einheitslänge willkürlich festlegt sowie das Wissen bezüglich des Schlusses vom Längenverhältnis auf das Flächenverhältnis.
Zurück zu Vietas Lösungsschritten - jetzt bezogen auf die umformulierte Aufgabe:
Schritt 1: Die bekannten wie auch die unbekannten Größen, die in dem Problemvorkommen, mit Buchstaben bezeichnen.
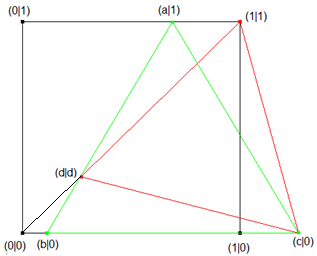
Schritt 2: Die Beziehungen zwischen diesen Größen in Gleichungen ausdrücken.
Diese Gleichungen ergeben sich jetzt aus den Längengleichheiten im gleichseitigen Dreieck und aus der Tatsache das H auf EG liegt.
Auch dieser Schritt setzt mathematische Kenntnisse voraus, welche einerseits die Abstandsberechnung zwischen zwei Punkten und andererseits die Herleitung einer Geradengleichung aus zwei Punkten sowie das Einsetzen eines dritten Punktes in diese Gleichung betreffen.
Schritt 3: Durch Umformungen die unbekannten Größen durch die bekannten ausdrücken.
Da a, b, c und d unbekannt sind, muss ein System von vier Gleichungen mit vier Unbekannten gelöst werden.
Bei fast jeder erfolgreichen Lösung bedarf es neben der Kenntnis der genannten Lösungsmethoden auch der Anwendung von Sätzen und Algorithmen der Mathematik. Das ist nicht neu aber einigen Schüler*innen, zum Beispiel Fragesteller*innen in diesem Forum, unbekannt. Sie schreiben dann: „Bitte die ganze Aufgabe lösen, ich verstehe nix.“