Geometrische Winkelberechnung im Innern eines Quadrats

Question

"Im Innern eines Quadrates ABCD liege der Punkt P so, dass Winkel DCP = Winkel CAP = 25° gilt. Wie groß ist der Winkel PBA?"

Answer 1

Die Antwort auf diese FRage geht fast nur Zeichnerisch,

die Strecke CA  ⇒   d= a√2 ist die Diagonale des Quadrates

Comments

Ich check immer noch nicht wie man da jetzt auch alpha kommt... also soweit mit der winkelhalbierende CA war ich auch schon, aber das hilft mir doch nicht alpha zu  bekommen oder?

---

Aus der Antwort geht wohl hervor das Akelei es nur zeichnerisch gelöst hat und nicht aus einer mathematischen Herleitung. Diese ist aber im Bundeswettbewerb der Mathematik erforderlich. Daher wird eine zeichnerische Bestimmung nicht gewertet.

Aufgrund der Fairness sollten hier dazu aber keine weiteren Lösungen veröffentlicht werden.

Answer 2

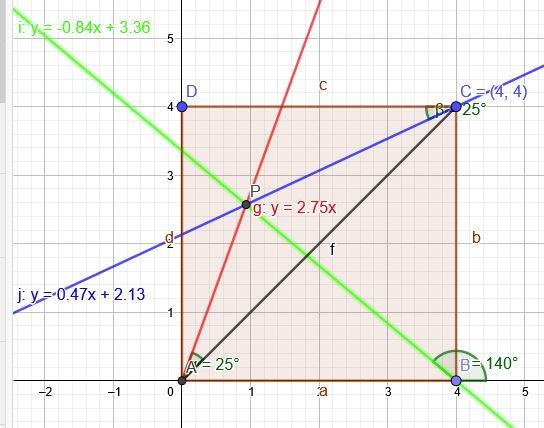
Berechnung rote Gerade:

\(y=tan(45°+25°) \cdot x≈2,747x\)

Berechnung blaue Gerade :

Der Wechselwinkel bei C ist \(25°\).

Punkt-Steigungsform der Geraden durch \(C(4|4)\):

\( \frac{y-4}{x-4}=tan(25°)≈0,466 \)

\( y=0,466 (x-4)+4=0,466 x+2,136\)

Berechnung von P:

\(2,747x=0,466 x+2,136\)

\(x≈0,936\)   \(y≈2,747 \cdot 0,936=2,57\)

Steigung der Geraden  durch B\( (4|0)\)  und P \((0,936|2,57)\)

\( \frac{2,57-0}{0,936-4}=m \)

\( m=-0,84\)    \( \tan^{-1}(-0,84 )=-40°\)

Der gesuchte Winkel ist \(40°\) groß.

Comments

Der gesuchte Winkel ist \(40°\) groß.

das ist korrekt, aber Deine Rechnung zeigt lediglich, dass der gesuchte Winkel ungefähr(!) 40° groß ist. Im Rahmen der von Dir verwendeten Genauigkeit.

Um die Identität \(=40°\) zu zeigen, hättest Du Dich schon durch die Additionstheoreme des Tangens mühen müssen.

Einfacher ginge es so:

Man betrachte den Kreis \(k\) (schwarz) mit Mittelpunkt \(B\) und Radius \(|AB|\). Es ist leicht zu zeigen, dass \(\angle APC = 135°\) (gelb) und damit halb so groß wie der dazugehörige Mittelpunktswinkel \(\angle ABC = 270°\) (blau) ist. Also liegt \(P\) auf \(k\) und \(\triangle ABP\) ist ein gleichschenkliges Dreieck.

Aus \(\angle BAP = 45°+25°=70°\) folgt unmittelbar:

\(\angle PBA = 180° - 2\cdot 70° = 40°\)

---

Danke dir für die Erläuterungen.