Achteck und Quadrat in der Mathe Didaktik

Question

Aufgabe: Achteck und Quadrat Mathematik Didaktik

Problem/Ansatz:

Hallo zusammen,

leider bin ich bei den folgenden Aufgaben vollkommen überfordert. Weder komme ich ansatzweise auf die Lösung des gefärbten Anteils noch kann ich meine nicht vorhandene Lösung an die jahrgangstufen anpassen.

Zu 2:

Die Größe der überlappten Fläche sollte gleichbleiben. Dies kann ich aber gerade nicht beweisen.....

enaktiv könnte man die überlappenden Quadrate nachbauen ( ausschneiden) und mit einer Stecknadel befestigen und dann ( sollte meine Idee richtig sein) das Quadrat drehen und die Flächeninhalte der entstehenden Überlappungen berechnen ( bei Kästchenpapier abzählen). Wie das ganze ikonisch klappen soll, weiß ich nicht.

Leider muss ich diese Vorlesung und Übung aufgrund diverser Überschneidungen in Alleinarbeit bearbeiten / dieses 1. Blatt haben wir ohne eine vorherige Vorlesung bekommen und muss in Eigenarbeit recherchiert und bearbeitet werden. Ich bin dankbar für jede Hilfe.

Text erkannt:

Aufgabe 1 (6 Punkte)
Betrachten Sie folgende Aufgabe:
In der Präsenzübung haben wir die Rolle der Anschaulichkeit und Strenge im Geometrieunterricht diskutiert. Zeigen Sie auf, inwiefern sich die verschiedenen Grade der Anschaulichkeit und Strenge in Lösungswegen zeigen können, indem Sie ...
a) ... diese Aufgabe auf dem Darstellungsniveau einer Klasse 6 anschaulich handelnd lösen.
b) ... diese Aufgabe auf dem Darstellungsniveau einer Klasse 7 lösen.
c) ... diese Aufgabe auf dem Darstellungsniveau einer Klasse 9 lösen.
Aufgabe 2 (6 Punkte)
In einem Schulbuch der Klasse 8 findet sich folgende Aufgabe:
Es ist ein Quadrat mit Mittelpunkt M ist gegeben. Ein zweites, gleichgroßes Quadrat ist mit einer Ecke in M befestigt und dreht sich um das erste Quadrat. Es ändert sich dabei zwar die Form der gemeinsamen Fläche, aber es bleibt auch eine Größe erhalten.
a) Von welcher Größe sollen die Schüler erkennen, dass sie unverändert bleibt?
b) Formulieren Sie einen Satz, der das Ergebnis der obigen Überlegungen beinhaltet.
c) Wie können Schüler:innen auf enaktiver und ikonischer Ebene zu einer Begründung oder einer Beweisidee gelangen?
d) Beweisen Sie den in Teil b) formulierten Satz exakt.

Answer 1

Hallo,

ich kann nun nicht wirklich beurteilen, welche Fähigkeiten Schüler der 6, 7. und 9. Klasse haben, aber um es mal 'ohne Formeln'*) zu machen, mache Dich mit dem regelmäßigem Achteck vertraut:

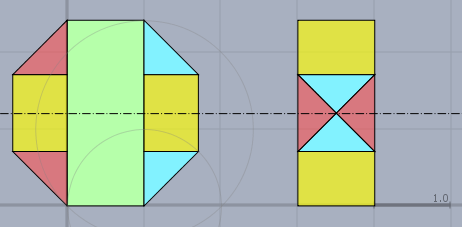
schneide das mittige Rechteck (grün) heraus, zerlege die abgeschnittenen Seiten in 2 Rechtecke (gelb) und vier Dreiecke (blau & rot) und ordne sie neu an. Ich überlasse es Dir zu beurteilen, dass das neu entstandene Rechteck genauso groß ist, wie das grüne Rechteck links.

Daraus folgt, dass das grüne Rechteck genau halb so groß ist, wie das Achteck.

Zeichne nun das schwarze Dreieck aus der Aufgabenstellung ein, teile es dabei entlang seiner Symmetrieachse:

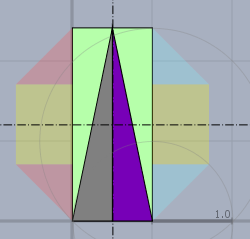
Es enstehen offensichtlich 4 identische Dreiecke gleicher Größe. Das 'schwarze' Dreieck nimmt folglich die halbe Fläche des Rechtecks und damit ein Viertel der Fläche des Achtecks ein.

zu Aufgabe 2)

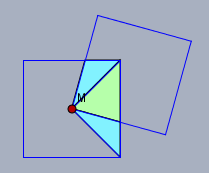
die blauen Dreiecke sind identisch. Was kann man dann über die Größe der gemeinsamen Fläche der beiden Quadrate sagen?

Falls Du noch Fragen hast, so melde Dich bitte.

*) Formeln werden sowieso völlig überbewertet ;-)

Comments

Hallo Werner-Salomon,

erstmal vielen Dank für deine freundliche, ausführliche und hilfreiche Antwort. Hättest du denn bei a ) auch einen Ansatz mit Formeln und ohne "Bastelei"= meiner Auffassung nach müsste die Lösungsmethode der 7. Klasse halt durch eine normale Beweisführung mit Flächeninhalten und Winkeln sein und in der 9. Klasse eventuell Strahlensätze ( falls die hier hilfreich sind)

zu 2 nach der Reihenfolge)

Ist die Fläche die gleich bleibt eventuell auch ein Viertel der Quadratsgröße?

a) Die Schüler sollen erkennen, dass die Größe der gemeinsamen Fläche gleich bleibt.

b) Überlappen sich zwei beliebige gleich große Quadrate Q1 und Q2 wobei M von Q1 gleich ein Eckpunkt von Q2 ist, so bleibt die Größe dieser Fläche bei beliebiger Drehung von Q2 um M immer gleich ?

---

folgende Alternativen bieten sich an :

 

---

Könntest du mir sie eventuell erläutern ?

---

Zum Achteck:

Das dunkelbraune Dreieck ist 1/8 des Achtecks. Das große Dreieck hat die doppelte Höhe und ist doppelt so groß, also 2*1/8=1/4 des Achtecks.

Zum Quadrat:

Wenn das rotierende Quadrat vervierfacht wird, erkennt man vier kongruente Teilflächen des festen Quadrats.

---

Upps Schreibfehler, ich meinte die 2. Alternative

---

Ich brauche für Aufgabe 1 ja noch eine Möglichkeit der 7. und 9. Klasse, die Verdoplung des kleinen Dreiecks würde ich dann eher bei der 7. Klasse einordnen, aber was mache ich bei der 9. Klasse welchen Lösungsweg gibt es noch ?

---

Hättest du denn bei a ) auch einen Ansatz mit Formeln und ohne "Bastelei" ...

Zum einen ist das keine "Bastelei" sondern IMHO Mathematik und zum anderen wundert mich die Frage Deinerseits angesichts der Vorlage, die ich Dir geliefert habe.

Nehme das Bild des Achtecks in meiner Antwort. Die kleinste Fläche ist ein rechtwinkliges und gleichschenkliges Dreieck (die roten & blauen). Die Länge der Hypotenuse ist die Kantenlänge des Achtecks, ich nenne sie \(a\).

Die einzige 'Formel', die Du hier brauchst, ist der Satz des Pythagoras. Und damit lässt sich dann die Länge \(b\) einer Kathete dieses Dreiecks berechnen:$$b = \frac12 \sqrt2\,a$$Alle anderen Längen der verbleibenden Flächen sind entweder \(a\) oder \(b\) oder Summen dieser Strecken. Wenn man deise Flächen ausrechnet und zusammen zählst, kommt man zur Fläche \(A_8\) des Achtecks:$$A_8=(2+2\sqrt2)a^2$$Das schwarze Dreieck aus der Aufgabenstellung hat die Grundseite \(a\) und die Höhe \(h=2b+a=(1+\sqrt2)a\). Also ist seine Fläche \(A_{\triangle}\):$$A_{\triangle}=\frac12(1+\sqrt2)a^2 = \frac14A_8$$Sobald die Schüler den Satz des Pythagoras kennen, ist dieser Weg derjenige, den ich als den 'klassischen Weg' bennenen würde. Wenn der Pythagoras erst in der 9.Klasse bekannt ist (ist das so?), dann wäre dies der Weg für die 9.Klasse.

---

Danke für deine Antwort, ich konnte die Aufgabe damit hoffentlich zufriedenstellend lösen