Welche Funktion ist in dem folgenden Schaubild mit logarithmischer Skalierung durch die Gerade dargestellt?

Question

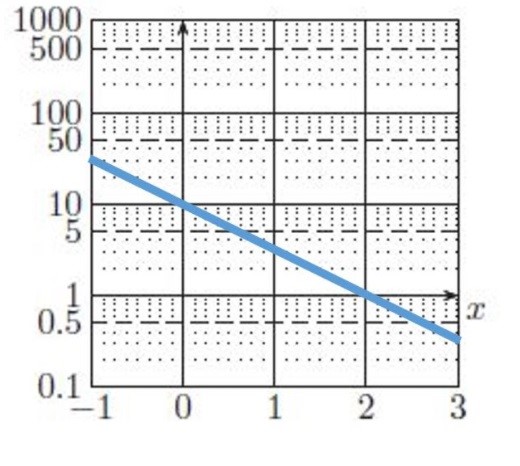
Aufgabe:

Welche Funktion ist in dem folgenden Schaubild mit logarithmischer Skalierung durch die Gerade dargestellt? Geben Sie die Funktionsvorschrift in der Variablen x ein.

Problem/Ansatz:

Leider keinen, da nicht mal der Ansatz bzw. der Rechenweg bekannt ist.

Answer 1

Geraden bei logarithmischer Skalierung gehören zu

Exponentialfunktionen der Art f(x)=a*b^x

Hier ist f(0)=10 also a=10  und f(2)=1 also 1 = 10*b^2

==> b=√0,1 ≈ 0,316

Also f(x) = 10* (√0,1)^x

Comments

Also f(x) = 10* (√0,1)^x

alternativ:$$f(x)= 10^{1-\frac x2}$$

Answer 2

Der Graph einer Exponentialfunktion ist in Verbindung mit einer logarithmischen senkrechten Skala eine Gerade.

Bei einer logarithmischen waagrechten Skala wären Logarithmusfunktionen eine Gerade. Es gibt auch noch doppeltlogarithmische Skalen (beide Achsen logarithmisch). Dort werden Potenzfunktionen als Geraden dargestellt.

Answer 3

Hallo

das muss y=a*b^x sein , da die Gerade fällt 0<b<1

a durch y(0)=10

b durch einen weiteren Punkt, überprüfen mit einem dritten

Gruß lul