Geogebra - Standardabweichung berechnen im CAS

Question

Hi! Ich war gerade dabei, ein Beispiel zur Normalverteilung mittels Geogebra zu lösen - ich habe das Ergebnis mit der Lösung, die rechnerisch ermittelt wurde, verglichen und bei meinem Ergebnis gab es eine kleine Abweichung, die ich mir nicht erklären kann..

die Aufgabe lautet: Es sei der IQ der Menschen Normalverteilt mit μ = 100 und σ = 15.

Wie groß müsste die Standardabweichung σ, bei gleichbleibendem Erwartungswert μ sein, sodass 80% der Menschen einen IQ von höchstens 120 haben?

Übrigens hab ich mit dem CAS-System mit dem Befehl "Normal( <Mittelwert>, <Standardabweichung>, <Wert der Variablen> ) gearbeitet und meine Werte folgendermaßen eingegeben:

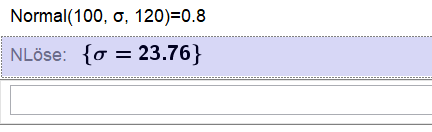
Text erkannt:

$\operatorname{Normal}(100, \sigma, 120)=0.8$
NLöse: $\{\sigma=23.76\}$

Geogebra rechnet {σ = 23.76} aus, wobei wobei es laut Lösung σ = 23.81 ist.

hier die Lösung: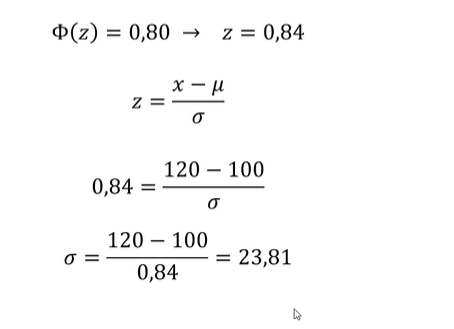

Text erkannt:

$\Phi(z)=0,80 \rightarrow \quad z=0,84$
$z=\frac{x-\mu}{\sigma}$
$0,84=\frac{120-100}{\sigma}$
$\sigma=\frac{120-100}{0,84}=23,81$

habe ich irgendetwas falsch eingegeben im CAS? Oder wie lässt sich diese Abweichung erklären? Vielen Dank im Voraus!

Answer 1

Die 0,84 sind nur auf zwei Stellen genau. Wenn du damit weiter rechnest, dann kannst du nicht erwarten, dass das Endergebnis auf vier Stellen genau ist.