Aufgabe:
Text erkannt:
Aufgabe mit Hilfsmitteln (40 Punkte)
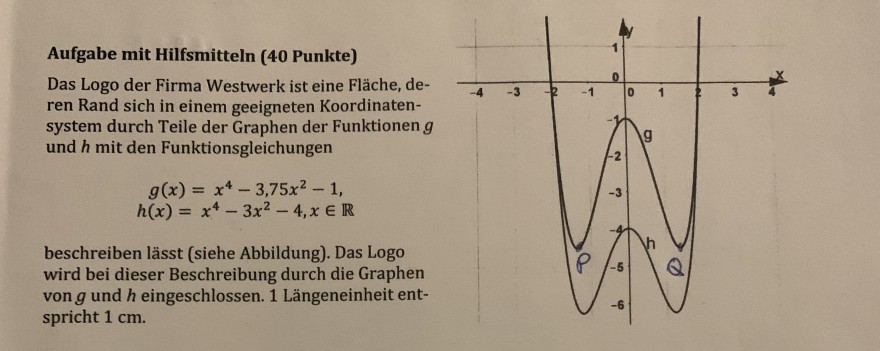
Das Logo der Firma Westwerk ist eine Fläche, deren Rand sich in einem geeigneten Koordinatensystem durch Teile der Graphen der Funktionen \( g \) und \( h \) mit den Funktionsgleichungen
\( \begin{array}{c} g(x)=x^{4}-3,75 x^{2}-1 \\ h(x)=x^{4}-3 x^{2}-4, x \in \mathbb{R} \end{array} \)
beschreiben lässt (siehe Abbildung). Das Logo wird bei dieser Beschreibung durch die Graphen von \( g \) und \( h \) eingeschlossen. 1 Längeneinheit entspricht \( 1 \mathrm{~cm} \).

Text erkannt:
Die Firmenleitung schlägt vor, das Logo leicht abzuändern. Das „Doppel-W" soll aber erhalten bleiben. Die Marketingabteilung experimentiert daraufhin mit Elementen der Funktionenschar \( f_{a} \) mit der Gleichung
\( f_{a}(x)=x^{4}+\left(a^{2}-4\right) x^{2}-4 a^{2}, a \geq 0 \)
als Begrenzungsfunktionen. Es gilt \( g(x)=f_{0,5}(x) \) und \( h(x)=f_{1}(x) \).
c) Weisen Sie nach, dass die Graphen der Funktionenschar \( f_{a} \) nur \( A(-2 \mid 0) \) und \( B(2 \mid 0) \) als gemeinsame Punkte besitzen.
(9 Punkte)
d) Untersuchen Sie die Graphen der Funktionenschar \( f_{a} \) in Abhängigkeit von a auf Wendestellen.
[Zur Kontrolle: Für die möglichen Wendestellen gilt \( \left.x=\sqrt{\frac{4-a^{2}}{6}} \vee x=-\sqrt{\frac{4-a^{2}}{6}} \cdot\right] \)
(14 Punkte)
e) Nach einem Vorschlag sollen als Begrenzungskurven die Graphen zweier Funktionen \( f_{a} \) und \( f_{a+0,5} \) gewählt werden. Außerdem soll die „größte Höhe" des Logos (Abstand der \( n \) Koordinaten" an der Stelle 0 ) \( 4 \mathrm{~cm} \) betragen.
Ermitteln Sie die Gleichungen der Begrenzungskurven des Logos.
(7 Punkte)
Problem/Ansatz:
Ich tu mir bei Funktionen Scharen echt schwer! Kann mir jemand diese Aufgaben (c, d, und e) vielleicht erklären? :)