Aufgabe:
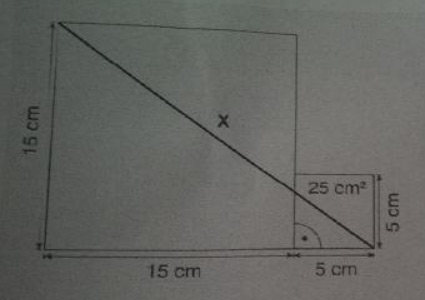
Für die Länge der Strecke \( x \) gilt einerseits:
\( x=\sqrt{15^{2}+20^{2}} \mathrm{~cm} \)
\( =\sqrt{225+400} \mathrm{~cm} \)
\( =\sqrt{625} \mathrm{~cm}=25 \mathrm{~cm} \)
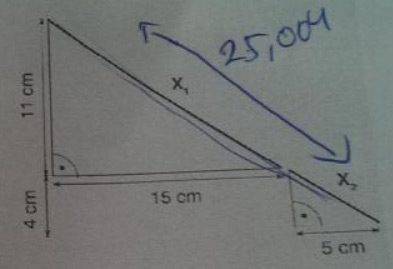
Andererseits, aufgeteilt in \( x_{1} \) und \( x_{2} \):
\( x_{1}=\sqrt{11^{2}+15^{2}} \mathrm{~cm}=\sqrt{346} \mathrm{~cm} \)
und \( x_{2}=\sqrt{4^{2}+5^{2}} \mathrm{~cm}=\sqrt{41} \mathrm{~cm} \)
\( a / s o \)
\( x=x_{1}+x_{2}=\sqrt{346} \mathrm{~cm}+\sqrt{41} \mathrm{~cm} \)
\( =25,004199, \ldots \mathrm{cm} \)
Dann mūsste ja eigentlich gelten \( 0=0,004199 \ldots \)
Wo liegt der Fehler?