Bestimmen Sie die Gleichungen der Tangenten an den Graphen von f in den Schnittpunkten mit den Koordinatenachsen.

Question

Aufgabe:

Text erkannt:

- 9 Gegeben ist die Funktion \( f \) mit \( f(x)=\frac{1}{20}(-2 x+1)^{5} \).

c) Bestimmen Sie die Gleichungen der Tangenten an den Graphen von \( f \) in den Schnittpunkten mit den Koordinatenachsen.

Problem/Ansatz:

hallo, kann jemand mir sagen, wie man Aufgabe c machen kann

Answer 1

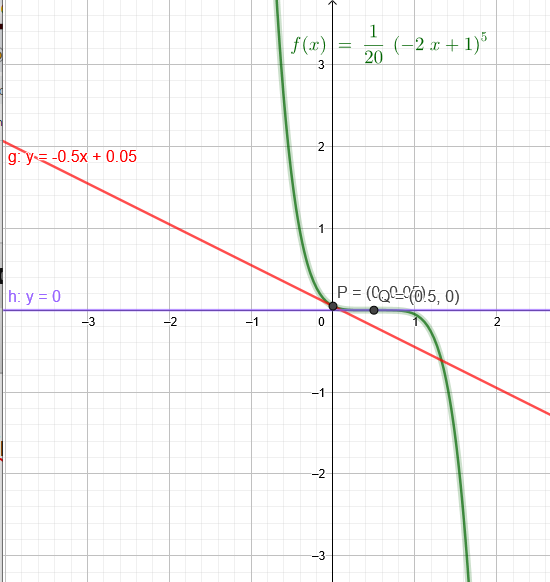
\( f(x)=\frac{1}{20}(-2 x+1)^{5} \)

Schnitt mit der y-Achse:

\( f(0)=\frac{1}{20}(-2*0+1)^{5} \)=\( \frac{1}{20} \)

Schnitt mit der x-Achse:

\( \frac{1}{20} \)(-2x+1)^5=0

(-2x+1)^5=0 |\( \sqrt[5]{} \)

-2x+1=0

x=\( \frac{1}{2} \)

Tangente in P(0|\( \frac{1}{20} \)):

f´(x)=\( \frac{1}{4} \)*(-2x+1)^4*(-2)

f´(0)=\( \frac{1}{4} \)*(-2*0+1)^4*(-2)=-\( \frac{1}{2} \)

Tangente: y=-0,5x+0,05

Tangente in Q(\( \frac{1}{2} \)|0):

f´(\( \frac{1}{2} \))=\( \frac{1}{4} \)*(-2*\( \frac{1}{2} \)+1)^4*(-2*\( \frac{1}{2} \))=0

y=0    x-Achse ist die Tangente