Berechnen Sie, wie viel Karton zur Herstellung der Verpackung mindestens benötigt wird.

Question

Aufgabe:

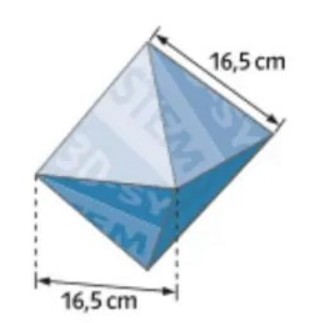
Alle Kanten dieser Verpackung sind gleich lang.

Berechnen Sie, wie viel \( \mathrm{cm}^{2} \) Karton zur Herstellung der Verpackung mindestens benötigt wird.

Problem/Ansatz:

Ich komme nicht so klar mit der Aufgabe. Wird die Oberfläche gesucht?

Answer 1

Berechne den Flächeninhalt der acht gleichseitigen Dreiecke.

Comments

Ich kenne nur die Formel: c*hc/2 ?

Aber von acht gleichseitigen Dreicke weiß nicht.

---

Das ist dann acht mal der Flächeninhalt eines Dreiecks.

Google flächeninhalt gleichseitiges dreieck

führt Dich zu

---

ahso okay. und die Höhe und c bleiben 16,5 oder wie ist das gemeint?

---

a ist die Seitenlänge.

---

stimmt :) seite a hat die Pyramide :)

Ok : dann 16,5^2 :4 und dann die 3 Wurzel = 117,88771

Vielen dank fürs Bild!

---

Das wäre falsch. Du sollst 8 mal A ausrechnen. Im Bild mit der Formel steht nicht die dritte Wuzel, sondern die Quadratwurzel von drei.

---

Hm wären es vielleicht 192,5 cm^?

---

moment:

a = 16,5 cm

Fomel lautet: a^2/4 * \( \sqrt{3} \)

16,5^2/4 * 1,732050808 = 117,89 ?

---

Nein.

8 * A = 8 * \( \frac{a^2}{4} \sqrt{3} \) = ...

---

vielen dank. Jetzt weiß ich was sie mit 8A meinen!

---

Warum 8 * A ? Wegen Innen- und Außenseiten der Seitenflächen? ;-)

---

Warum 8 * A ?

Weil es ein Oktaeder ist?

---

Danke, aber ich habe keinen Oktaeder gesehen (wohl weil ich solche Verpackungen noch nie im Handel gesehen habe), sondern die etwas mißlungene Darstellung einer quadratischen Pyramide, so wie Moliets wohl auch. ;-)

---

ich lerne immer etwas dazu. Es ist also ein Okteader. Warum lernen wir sowas in der Schule nicht?

---

Also ich sehe einen Oktaeder.

Oktaeder-Verpackung vgl. z.B. hier.

---

Danke, jetzt weiß ich, dass es solche Verpackungen auch im Handel gibt.

Ich wohne halt auf dem Land, habe wenig Fantasie und komme nicht viel herum.

---

Man kann beide Möglichkeiten erkennen.

-Seitenansicht eines Oktaeders
oder
- Draufsicht einer Pyramide
mit der Pyramidenspitze ausmittig.

Mir gelingt es zwischen beiden
Möglichkeiten hin-und herzuschalten

Answer 2

Das ist eine Pyramide mit quadratischer Grundfläche.

Ich zeichne diese Pyramide mal als Skizze:

Für die Dreiecksfläche benötigst du die Länge der Strecke von G zur Spitze.

Comments

Hat das etwas mit der Frage zu tun? Ich frage für eine Freundin.

Answer 3

Die Oberfläche Pyramide besteht 4
glechseitigen Dreiecken : Seitenlänge a = 16.5 cm
A = a^2 * √ 3 / 4
A = 117.888 cm^2

4 Stück 117.888 * 4 = 471.552 cm^2

Grundfläche : 16.5 ^2 = 272.25 cm^2

Zusammen 743,802 cm^2